- Регистрация
- 12.04.17
- Сообщения
- 19.095
- Реакции
- 107
- Репутация
- 0
Как подобрать лучшую экипировку в любимой игре? Конечно, можно банально перебрать все её возможные сочетания (например, для разбойника из World of Warcraft) и найти наилучшее. Без всякой магии и машинного обучения. Но можно ли добиться этого результата не «в лоб», а при помощи генетических алгоритмов, не примеряя каждую комбинацию? Интересно узнать, как размножаются и эволюционируют разбойники? Поехали.

Эта статья — углубление темы
Цель: показать интересующимся, как своими силами создать виртуальную популяцию игровых агентов, сталкивать их между собой, реализовать несложный генетический алгоритм (с мутациями) и визуализировать всё это при помощи HTML, CSS и Javascript.
Что нужно:
1. Python 3 + установить модуль
2. если захотите редактировать шаблон интерактивного отчёта, то базовое понимание HTML, CSS, JavaScript (jQuery).
ЭТАП 1 — ставим цель, разбираемся с ООП
Итак, конечная цель нашего кодинга — сделать так, чтобы к наилучшей экипировке можно было прийти при помощи симуляции генетики/эволюции/естественного отбора. И получить возможность визуально проследить этот путь.
Превратим нашу цель в конкретные задачи:
Здесь нам поможет ООП, создадим 4 фундаментальных класса:

ЭТАП 2 — заточка класса Rogue под размножение
договариваемся о терминах на берегу
В этой статье буду частить терминами «ген» (в коде — gene) и «генотип» (в коде — genotype). Также будут «мутации» (в коде — mutate, mutation), подразумевающие смену одним или несколькими генами своего значения. Размножение будет происходить просто путём «отпочковывания» потомка от родителя, поэтому

Итак, класс Rogue в сравнении с
1. Разбойник получает гены одним из возможных путей (был сгенерирован в самый первый день или унаследовал от «родителя» с мутацией или без оной). За это отвечают методы generate_random_genes, mutate_genes, mutate_gene:
код формирующих гены методов
# сгенерировать случайный набор генов (генотип):
def generate_random_genes(self):
dbg = DBG_rogue_generate_random_genes
self.my_genes[0] = randrange(0, len(RIGHT_HANDS)) # 1:
for x in genes_mutated:
genes_mutated_str += str(x) + ', '
else:
genes_mutated_str = str(genes_mutated[0])
print('\nf "mutate_genes" окончена:' + '\n\told genes: ', end='')
print(parent_genes)
print('\tgenes_mutated: ' + genes_mutated_str)
print('\tnew genes: ', end='')
print(self.my_genes)
# произвести мутацию в указанном гене, изменив его значение на любое другое:
def mutate_gene(self, gene_id):
dbg = DBG_rogue_mutate_gene
current_value = self.my_genes[gene_id]
new_value = current_value
if dbg: # для отладки:
print('\nf "mutate_gene":' + '\n\tgene_id: ' + str(gene_id) + '\n\told gene value: ' + str(current_value))
tries = 0
while new_value == current_value:
if dbg and tries > 0: # для отладки:
print('\tw2, because ' + str(new_value) + ' = ' + str(current_value) )
new_value = randrange(0, len(LINKS_TO_EQUIP_DICTS[gene_id]))
self.my_genes[gene_id] = new_value
tries += 1
if dbg: # для отладки:
print('\tnew gene value: ' + str(new_value) + '\n\ttries: ' + str(tries))
2. Гены (генотип) определяют, какую экипировку разбойник наденет (сразу же прирождении инициализации объекта). Для этого вызывается метод apply_genes:
apply_genes
# "применить" гены (генотип) путём надевания обусловленной ими экипировки:
def apply_genes(self):
dbg = DBG_rogue_apply_genes
pointer = 0
for item_id in self.my_genes:
self.wear_item(pointer, item_id, LINKS_TO_EQUIP_DICTS[pointer])
pointer += 1
if dbg: # для отладки:
print('\nf "apply_genes":' + '\n\tприменено.')
print(self)
3. Экипировка определит конечное значение «рейтинга» разбойника. Для этого будет вызван метод calculate_rate, который рассчитывает математическое ожидание урона:
calculate_rate
# метод для расчёта собственного рейтинга:
def calculate_rate(self):
dbg = DBG_rogue_calculate_rate
# вычислить вероятность попадания:
p_hit = self.stat_hit / 100
# вычислить вероятность скользящего и НЕскользящего удара:
p_glancing = self.stat_glancing_percent / 100
not_p_glancing = 1 - self.stat_glancing_percent / 100
# вычислить вероятность критического и НЕкритического удара:
p_crit = self.stat_crit / 100
not_p_crit = 1 - self.stat_crit / 100
# вычислить ожидание модификатора:
expectation_modificator = p_hit * (p_glancing * 0.7 + not_p_glancing * (p_crit * 2 + not_p_crit))
# вычислить ожидание урона с таким модификатором:
expectation_damage = expectation_modificator * self.stat_attackpower
expectation_damage = round(expectation_damage, 3)
if dbg:
print('\tожидание модификатора =', expectation_modificator)
print('\tожидание урона =', expectation_damage)
return expectation_damage
4. Рейтинг разбойника и будет определяющим фактором, ведущим к размножению или позорной смерти. Для этого введено понятие «победа» (метод embody_win) и «поражение» (метод embody_defeat):
embody_win и embody_defeat
# оформить победу в дуэли:
def embody_win(self):
dbg = DBG_rogue_embody_win
self.my_wins += 1
stats.genes_add_win(self.my_genes)
# после каждой второй победы:
if self.my_wins % population.wins_to_reproduce == 0:
# определить число рождаемых потомков:
total_borns = choice(population.possible_birth_quantities)
if dbg:
print('рождений будет ' + str(total_borns))
for x in range(0, total_borns):
if dbg:
print(self.name + ' рожает потомка...')
# родить разбойника-потомка:
new_rogue = Rogue(self.my_genes, self.my_generation, from_parent=True)
ROGUES_LIST.append(new_rogue)
Population.day_of_last_changes = current_day
# обновить рекорд количества побед у одного разбойника в популяции:
if self.my_wins > Population.record_max_wins:
Population.record_max_wins = self.my_wins
Population.max_winner_name = self.name
Population.max_winner_genes = self.my_genes
# оформить поражение в дуэли:
def embody_defeat(self):
dbg = DBG_rogue_embody_defeat
self.my_defeats += 1
# после двух поражений выпилиться:
if self.my_defeats == population.defeats_to_die:
self.alive = False
Population.how_many_rogues_alive -= 1
Population.day_of_last_changes = current_day
if dbg:
print(self.name + ' выпиливается...')
Ну и соответствующим образом переработан конструктор класса, чтобы работала эта цепочка «гены — экипировка — рейтинг»:
конструктор класса Rogue
def __init__(self, genes_list_inherited, parent_generation, from_parent=True, genes_can_mutate=True):
# инициализация списка слотов экипировки, который должен содержать id надетых предметов:
# 0 - правая рука, 1 - левая рука, 2 - перчатки, 3 - голова, 4 - грудь, 5 - штаны, 6 - обувь
self.equipment_slots = [0] * 7
# инициализация списка слотов экипировки, который должен содержать названия надетых предметов:
self.equipment_names = ['ничего'] * 7
# БАЗОВЫЕ значения характеристик (они - точка отсчёта при смене экипировки):
self.basic_stat_agility = 50
self.basic_stat_power = 40
self.basic_stat_hit = 80
self.basic_stat_crit = 20
self.basic_stat_mastery = 0
# рассчитать текущие характеристики без вещей:
self.set_stats_without_equip()
# статистические счётчики:
Population.how_many_rogues += 1
Population.how_many_rogues_alive += 1
# номер поколения:
self.my_generation = parent_generation + 1
if self.my_generation > Population.generations:
Population.generations = self.my_generation
# "имя" разбойника:
self.name = '"' + str(Population.how_many_rogues) + '-й, из поколения ' + str(parent_generation + 1) + '"'
# жив ли:
self.alive = True
# счётчики побед и поражений:
self.my_wins = 0
self.my_defeats = 0
# инициализировать цепочку генов:
self.my_genes = [0] * 7
if genes_can_mutate:
# если этот разбойник порождён другим разбойником, его гены должны незначительно мутировать:
if from_parent:
self.mutate_genes(genes_list_inherited)
else:
self.generate_random_genes()
else:
self.my_genes = genes_list_inherited
# отобразить эти гены в статистике:
stats.genes_add_presence(self.my_genes, self.my_generation)
# надеть экипировку согласно полученным генам:
self.apply_genes()
Подытожу эту логику класса картинкой:

ЭТАП 3 — классы Population, Stats и Challenge
Класс Population нужен лишь для трёх вещей:
class Population
class Population():
"""Класс используется для работы с популяцией."""
how_many_rogues = 0 # 0:
# создать нового разбойника, передав "пустой генотип" и отметку о том, что ему нужно сгенерировать гены:
new_rogue = Rogue('', 0, from_parent=False)
# пополнить список разбойников:
ROGUES_LIST.append(new_rogue)
total -= 1
# вывести актуальную информацию о популяции:
def __str__(self):
text = 'Популяция:\n'
text += 'поколений: ' + str(Population.generations) + '\n'
text += 'всего агентов: ' + str(Population.how_many_rogues) + '\n'
text += 'живых агентов: ' + str(Population.how_many_rogues_alive) + '\n'
text += 'рекорд побед: ' + str(Population.record_max_wins) + '\n'
text += 'имя рекордсмена: ' + str(Population.max_winner_name) + '\n'
text += 'генотип рекордсмена: ' + str(Population.max_winner_genes) + '\n'
return text
# перезагрузить популяцию, оставив в ней how_many_to_save разбойников с наиболее успешными генотипами:
def reload(self, how_many_to_save):
# обнулить кол-во разбойников:
Population.how_many_rogues_alive = 0
# "убить" всех существующих разбойников:
for x in ROGUES_LIST:
x.alive = False
# извлечь из словаря генотипов данные о лучших генотипах:
list_genotypes_top = stats.get_ordered_list_from_dict(LIST_FOR_DICTS_GENOTYPES[current_stage], inner_index=2)
# наполнить популяцию разбойниками с этими генотипами:
for x in range(0, how_many_to_save):
# преобразовать генотип из строки в список:
genotype_in_str = list_genotypes_top[x][0]
genotype_in_list = []
for char in genotype_in_str:
if char != '-':
genotype_in_list.append( int(char) )
# создать нового разбойника, передав генотип и отметку о том, что гены НЕ должны мутировать:
new_rogue = Rogue(genotype_in_list, 0, from_parent=True, genes_can_mutate=False)
# пополнить список разбойников:
ROGUES_LIST.append(new_rogue)
Класс Stats выполняет две основные задачи:
Забегая наперёд, показываю, как этот отчёт будет выглядеть:

Код HTML-шаблона для отчёта
Класс Stats также лучше просмотреть
Класс Challenger отвечает за симуляцию столкновений между случайно выбираемыми разбойниками. Каждый день вызывается метод perform_battles, который формирует из живых разбойников дуэльные пары и сталкивает их при помощи метода perform_battle, и в конце концов для каждого разбойника вызывается либо метод embody_win, либо метод embody_defeat. Кстати, если окажется, что произошла ничья (генотипы, а значит и рейтинги разбойников одинаковы), то они расходятся без последствий:
class Challenger
class Challenger():
"""Класс обеспечивает проведение боёв между случайными разбойниками."""
# провести серию боёв:
def perform_battles(self):
dbg = DBG_challenger_perform_battles
# создать список живых разбойников:
rogues_alive = []
for x in ROGUES_LIST:
if x.alive:
rogues_alive.append(x)
# перемешать список:
shuffle(rogues_alive)
# получить количество пар живых разбойников в популяции:
pairs_total = int(len(rogues_alive) // 2)
if dbg:
print('pairs_total =', pairs_total)
# запускать бои между соседними по списку разбойниками:
counter = 0
pointer = 0
while counter < pairs_total:
a_1 = rogues_alive[pointer]
a_2 = rogues_alive[pointer + 1]
self.perform_battle(a_1, a_2)
counter += 1
pointer += 2
# провести бой между двумя разбойниками:
def perform_battle(self, rogue_1, rogue_2):
dbg = DBG_challenger_perform_battle
if dbg:
print('\nновый бой между:', rogue_1.name, 'и', rogue_2.name)
# рассчитать рейтинг каждого разбойника (в более совершенной симуляции тут может быть полноценное сражение):
rating_1 = rogue_1.calculate_rate()
rating_2 = rogue_2.calculate_rate()
# счётчик боёв:
Population.how_many_battles += 1
if dbg:
print('\tих рейтинг:', rating_1, 'и', rating_2, 'соответственно.')
# раскидать очки между победителем и проигравшим:
if rating_1 > rating_2:
rogue_1.embody_win()
rogue_2.embody_defeat()
elif rating_1 < rating_2:
rogue_1.embody_defeat()
rogue_2.embody_win()
else:
Population.how_many_ties += 1
if dbg:
print('\tО чудо! Произошла ничья!')
Что ж, теперь переходим к телу программы, которое связывает воедино все упомянутые части кода. Сначала идут константы, которые определяют ключевые параметры симуляции: количество стадий, дней в стадии, начальное количество разбойников в популяции и т.д. Затем идут вспомогательные константы для отладки. И сами вызовы:
код для запуска симуляции
# КОНСТАНТЫ:
MAX_STAGES = 8 # методов):
DBG_rogue_mutate_genes = False
DBG_rogue_generate_random_genes = False
DBG_rogue_apply_genes = False
DBG_rogue_calculate_rate = False
DBG_rogue_mutate_gene = False
DBG_rogue_embody_win = False
DBG_rogue_embody_defeat = False
DBG_rogue_wear_item = False
DBG_challenger_perform_battles = False
DBG_challenger_perform_battle = False
DBG_days_report = False # продолжить цикл на доступное количество дней (1 день = 1 столкновение у каждого (почти*) разбойника)
# * - когда в популяции в какой-то день нечётное количество разбойников, кто-то из них остаётся без пары и не дерётся в этот день
while current_day DAY', current_day)
# выполнить серию соревнований:
challenger.perform_battles()
if DBG_days_report:
print('\nДень', current_day, 'завершён.')
print(population)
# статистика для этого дня:
stats.add_new_day(current_day)
# сколько дней подряд нет изменений в численности популяции:
if current_day - Population.day_of_last_changes > Population.max_days_without_changes:
Population.max_days_without_changes = current_day - Population.day_of_last_changes
# в конце каждого SLIDING_FREQUENCY дня (а также в первый и последний) отрисовывать слайды по распространённости генотипов:
if current_day % SLIDING_FREQUENCY == 0 or current_day == 1 or current_day == MAX_DAYS_AT_STAGE * MAX_STAGES:
stats.draw_genes_distribution(current_day)
# в конце каждого SLIDING_FREQUENCY дня (а также в первый и последний) отрисовывать слайды по победам генотипов:
if current_day % SLIDING_FREQUENCY == 0 or current_day == 1 or current_day == MAX_DAYS_AT_STAGE * MAX_STAGES:
stats.draw_genes_wins(current_day)
current_day += 1
# когда НЕпоследняя стадия подходит к концу, перезагрузить популяцию, оставив в ней указанное кол-во лучших генотипов:
if current_stage < MAX_STAGES - 1:
population.reload(ROGUES_AT_BEGIN)
current_stage += 1
# теперь понизить назад счётчик текущей стадии, чтобы удобно работать со списком LIST_FOR_DICTS_GENOTYPES:
current_stage -= 1
# вывести статистику дней:
print('\nДНИ:')
print(DICT_DAYS)
# нарисовать график о динамике одновременно живущих разбойников:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 1, 'живое население', 'дни', 'разбойников', 'charts/chart_population_demography.png')
# нарисовать график о динамике общей численности когда-либо живших разбойников:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 0, 'родившихся всего', 'дни', 'разбойников', 'charts/chart_population_total.png')
# нарисовать график о динамике разнообразия генотипов:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 2, 'разнообразие генотипов', 'дни', 'уникальных генотипов', 'charts/chart_genotypes_variety.png')
# нарисовать график о динамике ничьих (= столкновение одинаковых генотипов):
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 3, 'динамика ничьих', 'дни', 'ничьих', 'charts/chart_genotypes_ties.png')
# создать общий HTML для изучения сессии:
stats.create_index_html()
# вычислить затраченное время:
time_session = time() - time_begin
duration_info = 'работа программы длилась: ' + str(round(time_session, 2)) + ' сек.'
print('\n' + duration_info)
else:
print('__name__ is not "__main__".')
В конце симуляции в папке с программой сгенерируется файл с названием типа «report 2020-04-25_10-33-54.html». О нём подробнее в следующей части статьи.
ЭТАП 4 — визуализируем данные
Для дальнейших объяснений буду использовать такой набор экипировки:
evolution_equipment_obvious_strong.py
# Эти словари содержат перечни предметов соответствующего типа.
# Каждый элемент содержит кортеж, в котором значения означают следующее:
# 0 - название, 1 - атака, 2 - ловкость, 3 - сила, 4 - меткость, 5 - крит, 6 - мастерство
EQUIPMENT_COLLECTION = 'obvious_strong'
RIGHT_HANDS = dict()
RIGHT_HANDS[1] = ('Сильнейший меч', 5000, 0, 0, 0, 0, 0)
RIGHT_HANDS[2] = ('Средний меч', 800, 0, 0, 0, 0, 0)
RIGHT_HANDS[3] = ('Слабый меч', 20, 0, 0, 0, 0, 0)
LEFT_HANDS = dict()
LEFT_HANDS[1] = ('Сильнейший кинжал', 4000, 0, 0, 0, 0, 0)
LEFT_HANDS[2] = ('Слабый кинжал', 10, 0, 0, 0, 0, 0)
GLOVES = dict()
GLOVES[1] = ('Сильнейшие перчатки', 300, 0, 0, 0, 0, 0)
GLOVES[2] = ('Слабые перчатки', 1, 0, 0, 0, 0, 0)
HEADS = dict()
HEADS[1] = ('Сильнейший шлем', 300, 0, 0, 0, 0, 0)
HEADS[2] = ('Слабый шлем', 1, 0, 0, 0, 0, 0)
CHESTS = dict()
CHESTS[1] = ('Сильнейший нагрудник', 300, 0, 0, 0, 0, 0)
CHESTS[2] = ('Слабый нагрудник', 1, 0, 0, 0, 0, 0)
PANTS = dict()
PANTS[1] = ('Сильнейшие поножи', 300, 0, 0, 0, 0, 0)
PANTS[2] = ('Слабые поножи', 1, 0, 0, 0, 0, 0)
BOOTS = dict()
BOOTS[1] = ('Сильнейшие сапоги', 300, 0, 0, 0, 0, 0)
BOOTS[2] = ('Слабые сапоги', 1, 0, 0, 0, 0, 0)
Здесь возможных комбинаций наборов 192 (3 * 2 * 2 * 2 * 2 * 2 * 2). Соответственно, возможных генотипов будет тоже 192.
Главная идея визуализации: представить всё пространство возможных генотипов как прямоугольное поле, где каждый квадратик представляет отдельный генотип. Несложный алгоритм находит два средних делителя числа 192, это 16 и 12:
код этого алгоритма из конструктора класса Stats
# выписать в список все делители числа-суммы генотипов:
list_divisors = list()
current_number = int(self.genotypes_total // 2)
while current_number >= 2:
if self.genotypes_total % current_number == 0:
list_divisors.append(current_number)
current_number -= 1
print('list_divisors:', list_divisors)
# взять индекс примерно из середины полученного списка делителей:
somewhere_in_the_middle = len(list_divisors) // 2
# получить длины сторон будущего прямоугольника:
side_1 = list_divisors[somewhere_in_the_middle]
side_2 = self.genotypes_total / side_1
# определить, какая сторона длиннее, чтобы в будущем прямоугольник "положить" на бок:
self.side_x = int(side_1 if side_1 >= side_2 else side_2)
self.side_y = int(self.genotypes_total / self.side_x)
print('side_x =', self.side_x, 'side_y =', self.side_y)
Получаем область 16х12:

Список возможных генотипов генерируется этим кодом:
# создать список возможных генотипов:
self.list_of_possible_genotypes = list()
# для каждого оружия в правой руке:
for g1 in RIGHT_HANDS:
# для каждого оружия в левой руке:
for g2 in LEFT_HANDS:
# для каждых перчаток:
for g3 in GLOVES:
# для каждого шлема:
for g4 in HEADS:
# для каждого нагрудника:
for g5 in CHESTS:
# для каждых штанов:
for g6 in PANTS:
# для каждой обуви:
for g7 in BOOTS:
current_genotype = str(g1-1)+'-'+str(g2-1)+'-'+str(g3-1)+'-'+str(g4-1)+'-'+str(g5-1)+'-'+str(g6-1)+'-'+str(g7-1)
self.list_of_possible_genotypes.append(current_genotype)
Поэтому квадратики на поле представляют генотипы в таком порядке:
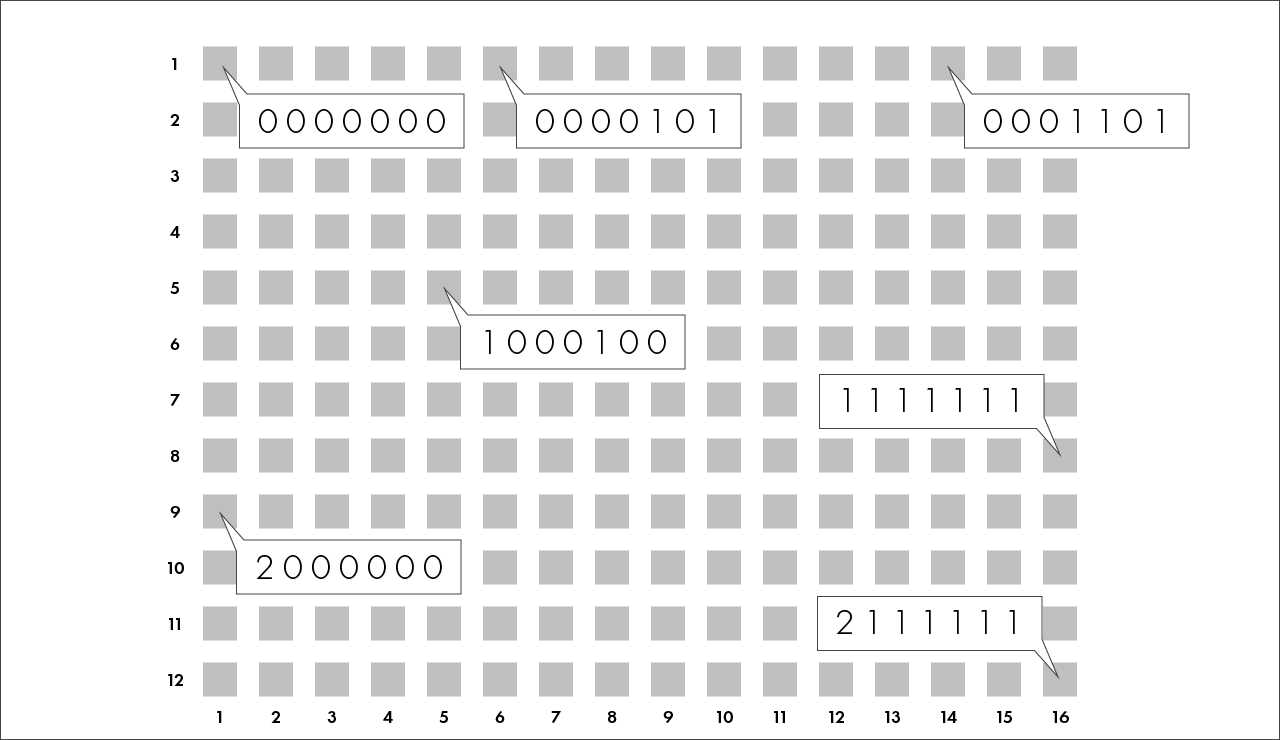
Это важная особенность, ведь, например, генотипы, которые содержат «ген Сильнейшего меча» (голубой уголок) находятся в верхней части поля, а те из них, которые также содержат «ген Сильнейшего кинжала» (синий уголок) — занимают ещё более верхнюю область:
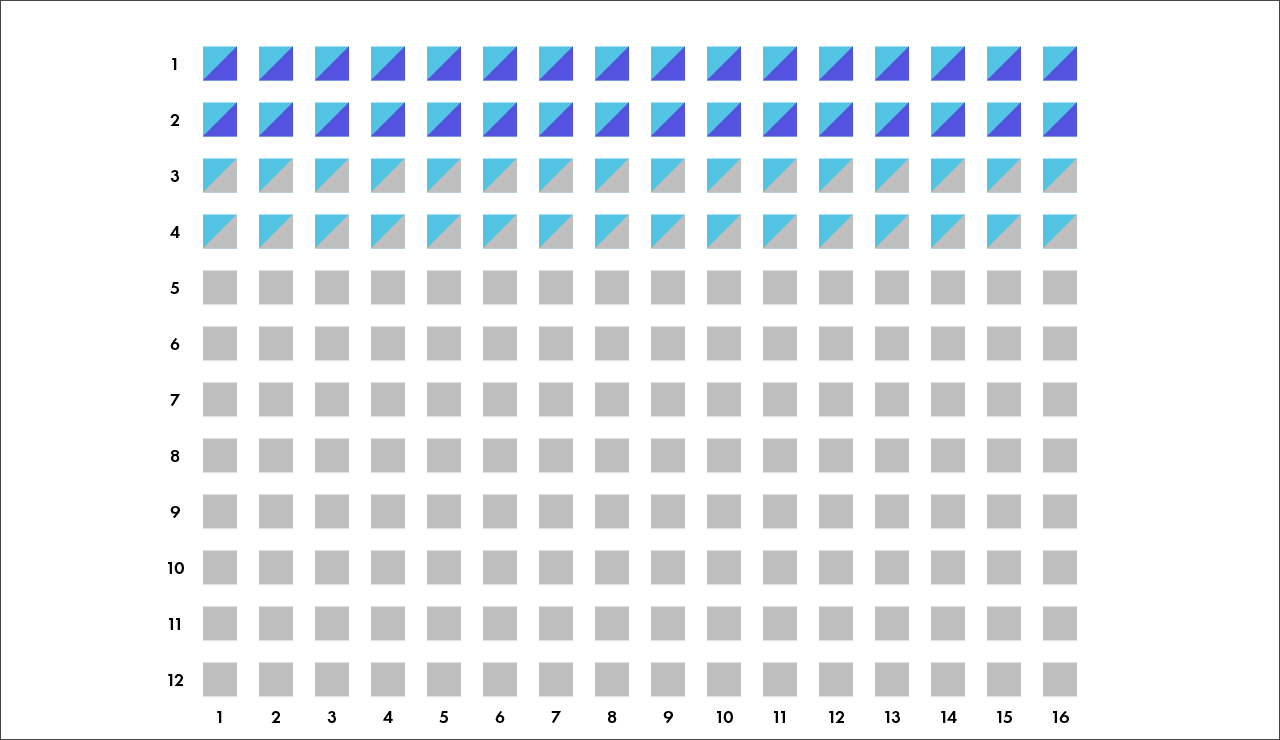
Таким образом, наиболее сильный генотип (0-0-0-0-0-0-0) находится в верхнем левом углу, а наиболее слабый (2-1-1-1-1-1-1) — в противоположном. Это поможет нам при наблюдении за развитием ситуации в динамике, ведь мы будем знать, что в процессе симуляции «доминирующий генофонд» должен смещаться в верхний левый угол поля:
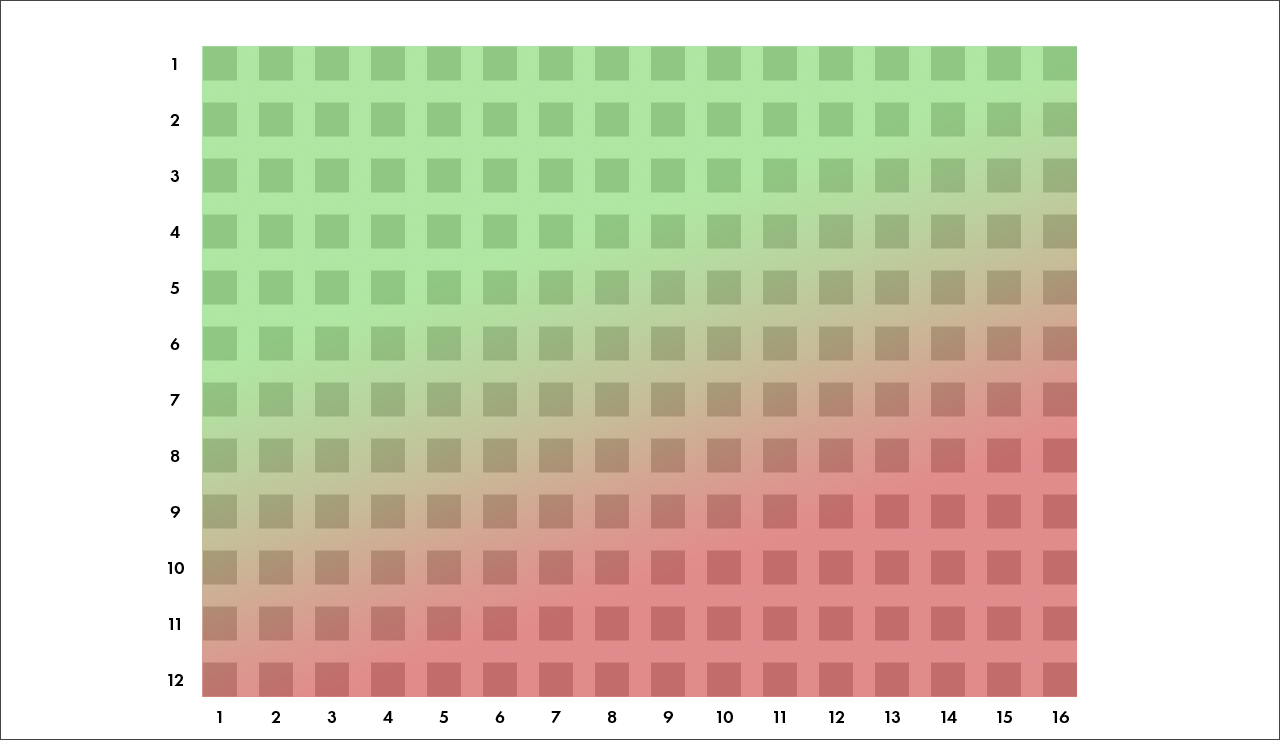
Теперь запустим симуляцию с такими параметрами:
MAX_STAGES = 5
MAX_DAYS_AT_STAGE = 40
SLIDING_FREQUENCY = 1
ROGUES_AT_BEGIN = 8
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1]
HTML_GSQUARE_SIDE = 16
HTML_GSQUARE_MARGIN = 3
То есть 8 разбойников на старте,
-контейнеры с полями (далее — слайды) создаются для каждого дня, 5 стадий по 40 дней. В итоге получим два набора слайдов по 200 штук: "распространённость генотипов" (сине-зелёные цвета) и "победы генотипов" (красные и зелёные цвета). Насыщенность цвета квадратиков зависит от значений.
Открываем сгенерированный HTML-отчёт и видим такую картину для 1-го и 10-го дня:
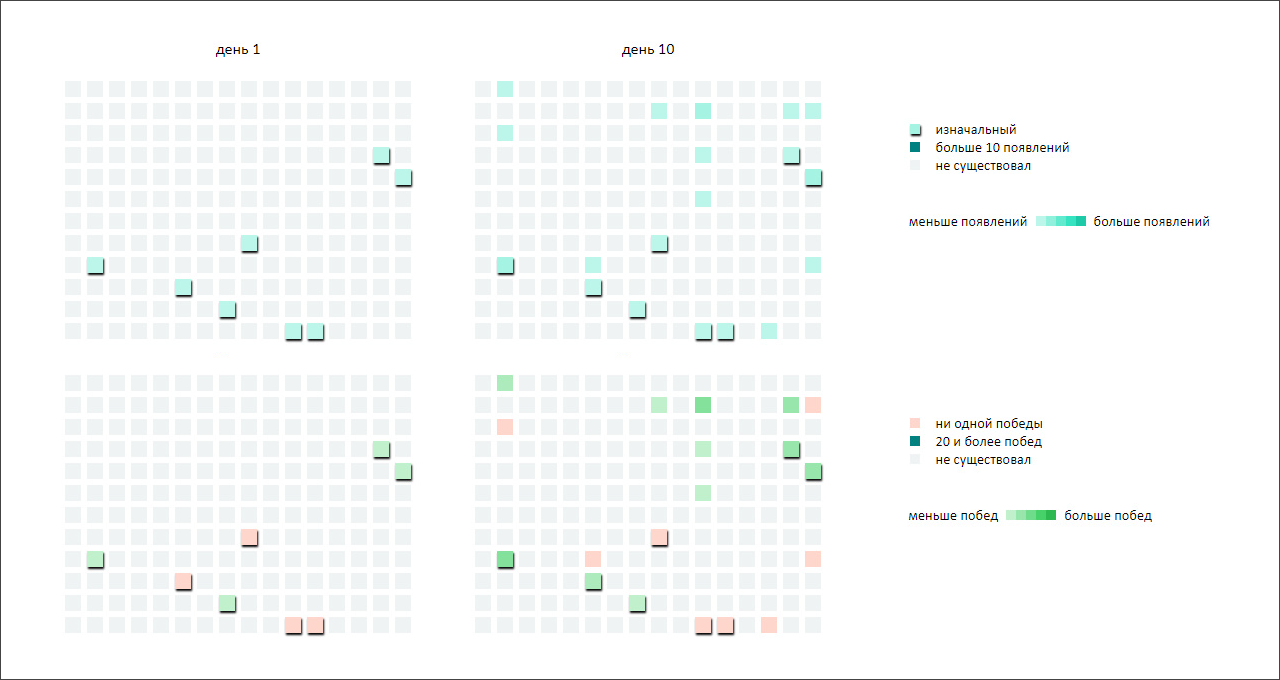
Итак, в первый день у нас сгенерировалось 8 разбойников, их квадратики до конца симуляции будут отбрасывать тень. Далее видим, что они начали драться, а значит, появляются первые победы, приводящие к размножению. Размножение с большой вероятностью сопряжено с мутациями, поэтому окрашенных квадратиков становится больше.
Заглянем в последующие дни. На 44-й день появился генотип "0-0-0-0-0-0-0" (см. за синей стрелкой). На 59-й день он уже вырвался вперёд по победам (см. за красной стрелкой).

На 137-й день видно, что "0-0-0-0-0-0-0" выбился в лидеры и по количеству появлений в популяции (см. за синей стрелкой). И на слайде последнего дня у него появилась золотая тень, так как он удержал за собой первое место по количеству побед.
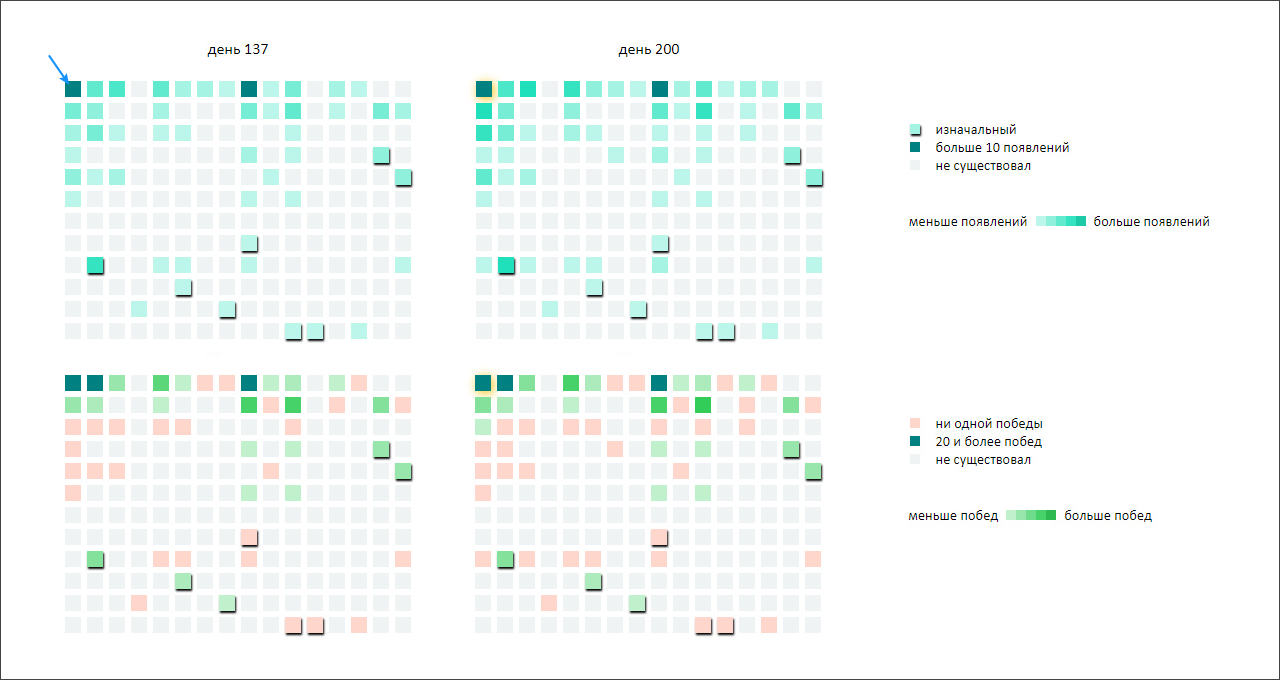
Как видим, действительно, естественный отбор смещает «генофонд» популяции влево и вверх, то есть в сторону более сильной экипировки. "Нижеправые" генотипы слабее "верхнелевых", поэтому они исчезают, едва появившись (красный цвет означает отсутствие побед). Более чётко это видно на большем масштабе:
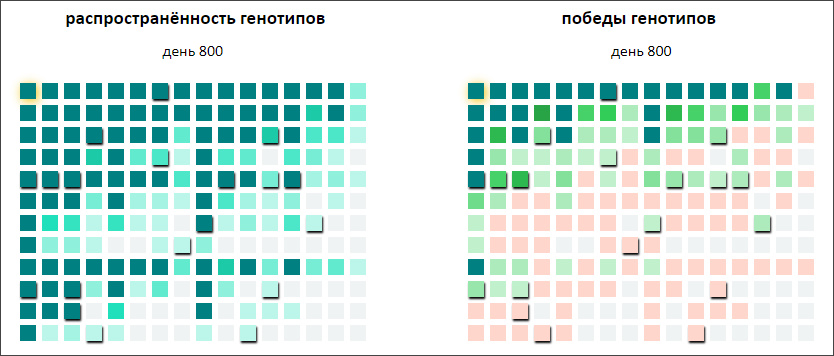
Ну и вердикт в отчёте выдан верный: генотип-победитель — 0-0-0-0-0-0-0:

Графики, полученные при помощи matplotlib, помогут дополнительно оценить происходящее:
1. график "живое население" показывает динамику изменения количества одновременно живущих разбойников;
2. график "родившихся всего" в основном близится к прямой линии, если не начать играться с демографическими параметрами:
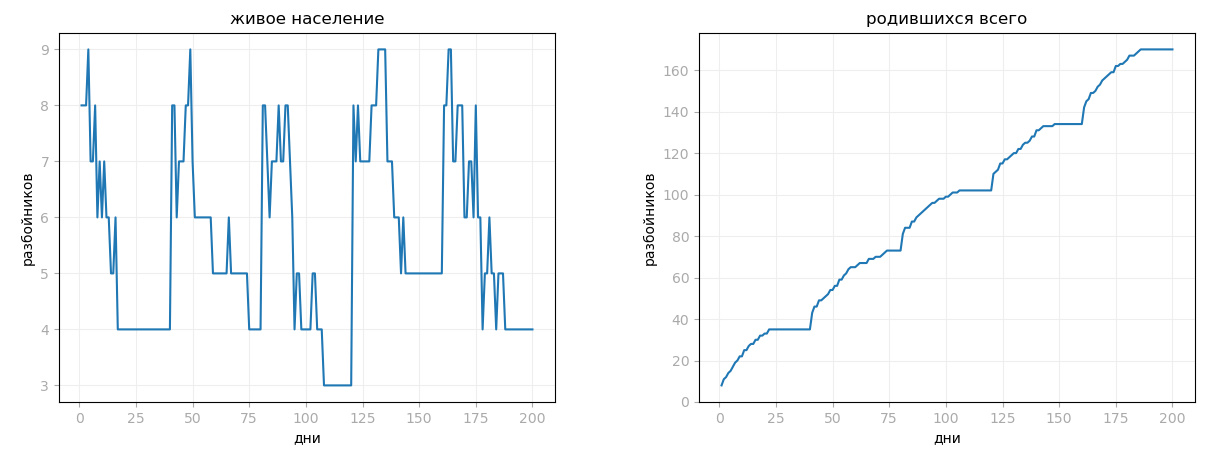
3. график "разнообразие генотипов" — обычно быстрый рост сначала, затем замедляется, постепенно приближаясь к максимуму;
4. график "динамика ничьих" — показывает, как с течением времени меняется количество ничьих (это бои, когда в бессмысленной схватке сталкиваются два одинаковых генотипа):

Бывает такое, что популяция «застаивается», когда в ней остаются разбойники с одинаковыми генотипами (на графиках наблюдается: резкий рост количества ничьих, неизменность в численности населения и численности уникальных генотипов).
Застой популяции означает, что вычисление и отрисовка слайдов происходит зря. Чтобы сократить периоды застоя, нужно снизить значение константы MAX_DAYS_AT_STAGE, и будет видно, что застой сократился, а местами вовсе исчез:

ЭТАП 5 — испытываем большие пространства генотипов
Теперь попробуем запустить симуляцию для рассматриваемого в
MAX_STAGES = 20
MAX_DAYS_AT_STAGE = 50
SLIDING_FREQUENCY = 10
ROGUES_AT_BEGIN = 8
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1, 2]
HTML_GSQUARE_SIDE = 10
HTML_GSQUARE_MARGIN = 3
Здесь паттерн распределения генотипов на слайдах будет иным, ведь наиболее значимая для общего результата экипировка («Меч Мастера») теперь находится в «других местах». Для визуализации этого набора экипировки уже характерно появление ряда «очагов силы» в разных местах, где сила экипировки выше, чем в соседних «районах».

Кстати, этот алгоритм безошибочно определил топовый набор экипировки (3-3-0-0-0-0-1), совпадающий с тем, который определялся комбинаторным алгоритмом с

И, наконец, я запустил тест для
с такими параметрами
MAX_STAGES = 30
MAX_DAYS_AT_STAGE = 50
SLIDING_FREQUENCY = 100
ROGUES_AT_BEGIN = 20
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1, 2]
HTML_GSQUARE_SIDE = 4
HTML_GSQUARE_MARGIN = 1

В общем, можно продолжать с этим забавляться, но остаётся неизменной тенденция: в ходе симуляции генотипы довольно быстро начинают скапливаться в этих самых «очагах силы». И доминирующий генотип оказывается в одном из самых ярких «очагов».
ЭТАП 6 — а имеет ли это всё смысл?
Если обратиться теперь к практической стороне вопроса, то нужно понять, способен ли этот генетический алгоритм найти правильный ответ ценой меньшего количества боёв, чем простой комбинаторный перебор всех генотипов. Ответ: да, способен. Доказательство под катом:
доказательство эффективности генетического алгоритма
Для этого вернёмся к набору экипировки на 1728 комбинаций.
Комбинаторному алгоритму достаточно подсчитать рейтинг экипировки по одному разу для каждой комбинации, т.е. 1728 раз.
Итак, генетический алгоритм должен найти ответ менее чем за 1728 таких же расчётов. Один «бой» между двумя разбойниками — это сразу 2 расчёта (для каждого из них). Итак, боёв должно быть не больше, чем 1728 / 2 = 864. Поехали.
Подобрал такие параметры:
MAX_STAGES = 8
MAX_DAYS_AT_STAGE = 20
SLIDING_FREQUENCY = 10
ROGUES_AT_BEGIN = 10
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1]
HTML_GSQUARE_SIDE = 10
HTML_GSQUARE_MARGIN = 3
Специально для наглядности выбрал результат, где начальные генотипы расположены подальше от будущего лидера 3-3-0-0-0-0-1:

Отчёт:

Итак, получилось прийти к ответу 3-3-0-0-0-0-1 за 547 боёв. Причём 87 боёв оказались напрасными (ничьи), что составляет 16% бесполезной работы.
На генофондах больших размеров выгода должна быть более ощутима.
P.S. На правильный ответ удаётся выйти даже при ROGUES_AT_BEGIN = 2 и POSSIBLE_BIRTH_QUANTITIES = [1]. Это кажется удивительным, ведь численность популяции ни разу не поднимается выше 2 разбойников. Потому что один проигрывает, другой выигрывает, первый умирает, а второй рождает одного потомка. И родитель начинает состязаться уже с этим потомком. Потомок либо сильнее, либо слабее. И таким образом движется безжалостное колесо отбора между родителем и его же потомком, пока не придёт в лучшую точку (которой сумеет достичь за отведённое время, поэтому это не всегда наилучшая).
Итоги
Весь код проекта я выложил на
Уважаемое сообщество, буду рад обратной связи по этой теме.

Эта статья — углубление темы
You must be registered for see links
, где уже описаны детали реализации персонажа и воздействия экипировки.Цель: показать интересующимся, как своими силами создать виртуальную популяцию игровых агентов, сталкивать их между собой, реализовать несложный генетический алгоритм (с мутациями) и визуализировать всё это при помощи HTML, CSS и Javascript.
Что нужно:
1. Python 3 + установить модуль
You must be registered for see links
; IDE (у меня PyCharm);2. если захотите редактировать шаблон интерактивного отчёта, то базовое понимание HTML, CSS, JavaScript (jQuery).
ЭТАП 1 — ставим цель, разбираемся с ООП
Итак, конечная цель нашего кодинга — сделать так, чтобы к наилучшей экипировке можно было прийти при помощи симуляции генетики/эволюции/естественного отбора. И получить возможность визуально проследить этот путь.
Превратим нашу цель в конкретные задачи:
- продумать и реализовать генетический механизм на уровне индивида («гены» разбойника должны прямо влиять на выбор экипировки)
- реализовать механизмы рождения потомков, передачи им генов, а также случайных незначительных мутаций, чтобы обеспечить вариативность и саму возможность поиска лучшего
- реализовать генетическое «состязание», отбор генов (сталкивать их носителей между собой, чтобы исход столкновения низвергал «плохие» гены и возносил «хорошие»)
- собрать всё в целостную систему, в которой разбойники смогут эволюционировать в идеальных бойцов
- собирать и визуализировать данные, чтобы было на что полюбоваться (а то интересно же!)
- оценить полезность этих занятий
Здесь нам поможет ООП, создадим 4 фундаментальных класса:

ЭТАП 2 — заточка класса Rogue под размножение
договариваемся о терминах на берегу
В этой статье буду частить терминами «ген» (в коде — gene) и «генотип» (в коде — genotype). Также будут «мутации» (в коде — mutate, mutation), подразумевающие смену одним или несколькими генами своего значения. Размножение будет происходить просто путём «отпочковывания» потомка от родителя, поэтому
You must be registered for see links
и других подобных усложнений не будет. Генотип разбойника — это список из 7 чисел, которые являются его генами:
Итак, класс Rogue в сравнении с
You must be registered for see links
существенно разрастается.1. Разбойник получает гены одним из возможных путей (был сгенерирован в самый первый день или унаследовал от «родителя» с мутацией или без оной). За это отвечают методы generate_random_genes, mutate_genes, mutate_gene:
код формирующих гены методов
# сгенерировать случайный набор генов (генотип):
def generate_random_genes(self):
dbg = DBG_rogue_generate_random_genes
self.my_genes[0] = randrange(0, len(RIGHT_HANDS)) # 1:
for x in genes_mutated:
genes_mutated_str += str(x) + ', '
else:
genes_mutated_str = str(genes_mutated[0])
print('\nf "mutate_genes" окончена:' + '\n\told genes: ', end='')
print(parent_genes)
print('\tgenes_mutated: ' + genes_mutated_str)
print('\tnew genes: ', end='')
print(self.my_genes)
# произвести мутацию в указанном гене, изменив его значение на любое другое:
def mutate_gene(self, gene_id):
dbg = DBG_rogue_mutate_gene
current_value = self.my_genes[gene_id]
new_value = current_value
if dbg: # для отладки:
print('\nf "mutate_gene":' + '\n\tgene_id: ' + str(gene_id) + '\n\told gene value: ' + str(current_value))
tries = 0
while new_value == current_value:
if dbg and tries > 0: # для отладки:
print('\tw2, because ' + str(new_value) + ' = ' + str(current_value) )
new_value = randrange(0, len(LINKS_TO_EQUIP_DICTS[gene_id]))
self.my_genes[gene_id] = new_value
tries += 1
if dbg: # для отладки:
print('\tnew gene value: ' + str(new_value) + '\n\ttries: ' + str(tries))
2. Гены (генотип) определяют, какую экипировку разбойник наденет (сразу же при
apply_genes
# "применить" гены (генотип) путём надевания обусловленной ими экипировки:
def apply_genes(self):
dbg = DBG_rogue_apply_genes
pointer = 0
for item_id in self.my_genes:
self.wear_item(pointer, item_id, LINKS_TO_EQUIP_DICTS[pointer])
pointer += 1
if dbg: # для отладки:
print('\nf "apply_genes":' + '\n\tприменено.')
print(self)
3. Экипировка определит конечное значение «рейтинга» разбойника. Для этого будет вызван метод calculate_rate, который рассчитывает математическое ожидание урона:
calculate_rate
# метод для расчёта собственного рейтинга:
def calculate_rate(self):
dbg = DBG_rogue_calculate_rate
# вычислить вероятность попадания:
p_hit = self.stat_hit / 100
# вычислить вероятность скользящего и НЕскользящего удара:
p_glancing = self.stat_glancing_percent / 100
not_p_glancing = 1 - self.stat_glancing_percent / 100
# вычислить вероятность критического и НЕкритического удара:
p_crit = self.stat_crit / 100
not_p_crit = 1 - self.stat_crit / 100
# вычислить ожидание модификатора:
expectation_modificator = p_hit * (p_glancing * 0.7 + not_p_glancing * (p_crit * 2 + not_p_crit))
# вычислить ожидание урона с таким модификатором:
expectation_damage = expectation_modificator * self.stat_attackpower
expectation_damage = round(expectation_damage, 3)
if dbg:
print('\tожидание модификатора =', expectation_modificator)
print('\tожидание урона =', expectation_damage)
return expectation_damage
4. Рейтинг разбойника и будет определяющим фактором, ведущим к размножению или позорной смерти. Для этого введено понятие «победа» (метод embody_win) и «поражение» (метод embody_defeat):
embody_win и embody_defeat
# оформить победу в дуэли:
def embody_win(self):
dbg = DBG_rogue_embody_win
self.my_wins += 1
stats.genes_add_win(self.my_genes)
# после каждой второй победы:
if self.my_wins % population.wins_to_reproduce == 0:
# определить число рождаемых потомков:
total_borns = choice(population.possible_birth_quantities)
if dbg:
print('рождений будет ' + str(total_borns))
for x in range(0, total_borns):
if dbg:
print(self.name + ' рожает потомка...')
# родить разбойника-потомка:
new_rogue = Rogue(self.my_genes, self.my_generation, from_parent=True)
ROGUES_LIST.append(new_rogue)
Population.day_of_last_changes = current_day
# обновить рекорд количества побед у одного разбойника в популяции:
if self.my_wins > Population.record_max_wins:
Population.record_max_wins = self.my_wins
Population.max_winner_name = self.name
Population.max_winner_genes = self.my_genes
# оформить поражение в дуэли:
def embody_defeat(self):
dbg = DBG_rogue_embody_defeat
self.my_defeats += 1
# после двух поражений выпилиться:
if self.my_defeats == population.defeats_to_die:
self.alive = False
Population.how_many_rogues_alive -= 1
Population.day_of_last_changes = current_day
if dbg:
print(self.name + ' выпиливается...')
Ну и соответствующим образом переработан конструктор класса, чтобы работала эта цепочка «гены — экипировка — рейтинг»:
конструктор класса Rogue
def __init__(self, genes_list_inherited, parent_generation, from_parent=True, genes_can_mutate=True):
# инициализация списка слотов экипировки, который должен содержать id надетых предметов:
# 0 - правая рука, 1 - левая рука, 2 - перчатки, 3 - голова, 4 - грудь, 5 - штаны, 6 - обувь
self.equipment_slots = [0] * 7
# инициализация списка слотов экипировки, который должен содержать названия надетых предметов:
self.equipment_names = ['ничего'] * 7
# БАЗОВЫЕ значения характеристик (они - точка отсчёта при смене экипировки):
self.basic_stat_agility = 50
self.basic_stat_power = 40
self.basic_stat_hit = 80
self.basic_stat_crit = 20
self.basic_stat_mastery = 0
# рассчитать текущие характеристики без вещей:
self.set_stats_without_equip()
# статистические счётчики:
Population.how_many_rogues += 1
Population.how_many_rogues_alive += 1
# номер поколения:
self.my_generation = parent_generation + 1
if self.my_generation > Population.generations:
Population.generations = self.my_generation
# "имя" разбойника:
self.name = '"' + str(Population.how_many_rogues) + '-й, из поколения ' + str(parent_generation + 1) + '"'
# жив ли:
self.alive = True
# счётчики побед и поражений:
self.my_wins = 0
self.my_defeats = 0
# инициализировать цепочку генов:
self.my_genes = [0] * 7
if genes_can_mutate:
# если этот разбойник порождён другим разбойником, его гены должны незначительно мутировать:
if from_parent:
self.mutate_genes(genes_list_inherited)
else:
self.generate_random_genes()
else:
self.my_genes = genes_list_inherited
# отобразить эти гены в статистике:
stats.genes_add_presence(self.my_genes, self.my_generation)
# надеть экипировку согласно полученным генам:
self.apply_genes()
Подытожу эту логику класса картинкой:

ЭТАП 3 — классы Population, Stats и Challenge
Класс Population нужен лишь для трёх вещей:
- создание популяции из указанного количества разбойников со случайными генами и биологическими параметрами, которые будут всегда неизменны (wins_to_reproduce — сколько побед разбойнику нужно одержать для размножения, defeats_to_die — сколько поражений заставят индивида умереть);
- «перезагрузка» популяции, т.е. когда заканчивается последний день текущей Стадии, все разбойники уничтожаются и создаются разбойники с наилучшими генотипами (см. метод reload);
- хранение некоторых данных о популяции для статистики.
class Population
class Population():
"""Класс используется для работы с популяцией."""
how_many_rogues = 0 # 0:
# создать нового разбойника, передав "пустой генотип" и отметку о том, что ему нужно сгенерировать гены:
new_rogue = Rogue('', 0, from_parent=False)
# пополнить список разбойников:
ROGUES_LIST.append(new_rogue)
total -= 1
# вывести актуальную информацию о популяции:
def __str__(self):
text = 'Популяция:\n'
text += 'поколений: ' + str(Population.generations) + '\n'
text += 'всего агентов: ' + str(Population.how_many_rogues) + '\n'
text += 'живых агентов: ' + str(Population.how_many_rogues_alive) + '\n'
text += 'рекорд побед: ' + str(Population.record_max_wins) + '\n'
text += 'имя рекордсмена: ' + str(Population.max_winner_name) + '\n'
text += 'генотип рекордсмена: ' + str(Population.max_winner_genes) + '\n'
return text
# перезагрузить популяцию, оставив в ней how_many_to_save разбойников с наиболее успешными генотипами:
def reload(self, how_many_to_save):
# обнулить кол-во разбойников:
Population.how_many_rogues_alive = 0
# "убить" всех существующих разбойников:
for x in ROGUES_LIST:
x.alive = False
# извлечь из словаря генотипов данные о лучших генотипах:
list_genotypes_top = stats.get_ordered_list_from_dict(LIST_FOR_DICTS_GENOTYPES[current_stage], inner_index=2)
# наполнить популяцию разбойниками с этими генотипами:
for x in range(0, how_many_to_save):
# преобразовать генотип из строки в список:
genotype_in_str = list_genotypes_top[x][0]
genotype_in_list = []
for char in genotype_in_str:
if char != '-':
genotype_in_list.append( int(char) )
# создать нового разбойника, передав генотип и отметку о том, что гены НЕ должны мутировать:
new_rogue = Rogue(genotype_in_list, 0, from_parent=True, genes_can_mutate=False)
# пополнить список разбойников:
ROGUES_LIST.append(new_rogue)
Класс Stats выполняет две основные задачи:
- сбор данных в процессе работы симуляции (например, показатели каждого дня: количество живых разбойников, количество уникальных генотипов и т.д.)
- визуализация данных (отрисовка графиков при помощи
You must be registered for see links, генерация интерактивного отчёта в формате HTML-страницы, которую можно будет открыть в браузере).
Забегая наперёд, показываю, как этот отчёт будет выглядеть:

Код HTML-шаблона для отчёта
You must be registered for see links
.Класс Stats также лучше просмотреть
You must be registered for see links
(а то больно много строк здесь окажется).Класс Challenger отвечает за симуляцию столкновений между случайно выбираемыми разбойниками. Каждый день вызывается метод perform_battles, который формирует из живых разбойников дуэльные пары и сталкивает их при помощи метода perform_battle, и в конце концов для каждого разбойника вызывается либо метод embody_win, либо метод embody_defeat. Кстати, если окажется, что произошла ничья (генотипы, а значит и рейтинги разбойников одинаковы), то они расходятся без последствий:
class Challenger
class Challenger():
"""Класс обеспечивает проведение боёв между случайными разбойниками."""
# провести серию боёв:
def perform_battles(self):
dbg = DBG_challenger_perform_battles
# создать список живых разбойников:
rogues_alive = []
for x in ROGUES_LIST:
if x.alive:
rogues_alive.append(x)
# перемешать список:
shuffle(rogues_alive)
# получить количество пар живых разбойников в популяции:
pairs_total = int(len(rogues_alive) // 2)
if dbg:
print('pairs_total =', pairs_total)
# запускать бои между соседними по списку разбойниками:
counter = 0
pointer = 0
while counter < pairs_total:
a_1 = rogues_alive[pointer]
a_2 = rogues_alive[pointer + 1]
self.perform_battle(a_1, a_2)
counter += 1
pointer += 2
# провести бой между двумя разбойниками:
def perform_battle(self, rogue_1, rogue_2):
dbg = DBG_challenger_perform_battle
if dbg:
print('\nновый бой между:', rogue_1.name, 'и', rogue_2.name)
# рассчитать рейтинг каждого разбойника (в более совершенной симуляции тут может быть полноценное сражение):
rating_1 = rogue_1.calculate_rate()
rating_2 = rogue_2.calculate_rate()
# счётчик боёв:
Population.how_many_battles += 1
if dbg:
print('\tих рейтинг:', rating_1, 'и', rating_2, 'соответственно.')
# раскидать очки между победителем и проигравшим:
if rating_1 > rating_2:
rogue_1.embody_win()
rogue_2.embody_defeat()
elif rating_1 < rating_2:
rogue_1.embody_defeat()
rogue_2.embody_win()
else:
Population.how_many_ties += 1
if dbg:
print('\tО чудо! Произошла ничья!')
Что ж, теперь переходим к телу программы, которое связывает воедино все упомянутые части кода. Сначала идут константы, которые определяют ключевые параметры симуляции: количество стадий, дней в стадии, начальное количество разбойников в популяции и т.д. Затем идут вспомогательные константы для отладки. И сами вызовы:
код для запуска симуляции
# КОНСТАНТЫ:
MAX_STAGES = 8 # методов):
DBG_rogue_mutate_genes = False
DBG_rogue_generate_random_genes = False
DBG_rogue_apply_genes = False
DBG_rogue_calculate_rate = False
DBG_rogue_mutate_gene = False
DBG_rogue_embody_win = False
DBG_rogue_embody_defeat = False
DBG_rogue_wear_item = False
DBG_challenger_perform_battles = False
DBG_challenger_perform_battle = False
DBG_days_report = False # продолжить цикл на доступное количество дней (1 день = 1 столкновение у каждого (почти*) разбойника)
# * - когда в популяции в какой-то день нечётное количество разбойников, кто-то из них остаётся без пары и не дерётся в этот день
while current_day DAY', current_day)
# выполнить серию соревнований:
challenger.perform_battles()
if DBG_days_report:
print('\nДень', current_day, 'завершён.')
print(population)
# статистика для этого дня:
stats.add_new_day(current_day)
# сколько дней подряд нет изменений в численности популяции:
if current_day - Population.day_of_last_changes > Population.max_days_without_changes:
Population.max_days_without_changes = current_day - Population.day_of_last_changes
# в конце каждого SLIDING_FREQUENCY дня (а также в первый и последний) отрисовывать слайды по распространённости генотипов:
if current_day % SLIDING_FREQUENCY == 0 or current_day == 1 or current_day == MAX_DAYS_AT_STAGE * MAX_STAGES:
stats.draw_genes_distribution(current_day)
# в конце каждого SLIDING_FREQUENCY дня (а также в первый и последний) отрисовывать слайды по победам генотипов:
if current_day % SLIDING_FREQUENCY == 0 or current_day == 1 or current_day == MAX_DAYS_AT_STAGE * MAX_STAGES:
stats.draw_genes_wins(current_day)
current_day += 1
# когда НЕпоследняя стадия подходит к концу, перезагрузить популяцию, оставив в ней указанное кол-во лучших генотипов:
if current_stage < MAX_STAGES - 1:
population.reload(ROGUES_AT_BEGIN)
current_stage += 1
# теперь понизить назад счётчик текущей стадии, чтобы удобно работать со списком LIST_FOR_DICTS_GENOTYPES:
current_stage -= 1
# вывести статистику дней:
print('\nДНИ:')
print(DICT_DAYS)
# нарисовать график о динамике одновременно живущих разбойников:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 1, 'живое население', 'дни', 'разбойников', 'charts/chart_population_demography.png')
# нарисовать график о динамике общей численности когда-либо живших разбойников:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 0, 'родившихся всего', 'дни', 'разбойников', 'charts/chart_population_total.png')
# нарисовать график о динамике разнообразия генотипов:
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 2, 'разнообразие генотипов', 'дни', 'уникальных генотипов', 'charts/chart_genotypes_variety.png')
# нарисовать график о динамике ничьих (= столкновение одинаковых генотипов):
stats.draw_and_put_line_chart_to_file(DICT_DAYS, 3, 'динамика ничьих', 'дни', 'ничьих', 'charts/chart_genotypes_ties.png')
# создать общий HTML для изучения сессии:
stats.create_index_html()
# вычислить затраченное время:
time_session = time() - time_begin
duration_info = 'работа программы длилась: ' + str(round(time_session, 2)) + ' сек.'
print('\n' + duration_info)
else:
print('__name__ is not "__main__".')
В конце симуляции в папке с программой сгенерируется файл с названием типа «report 2020-04-25_10-33-54.html». О нём подробнее в следующей части статьи.
ЭТАП 4 — визуализируем данные
Для дальнейших объяснений буду использовать такой набор экипировки:
evolution_equipment_obvious_strong.py
# Эти словари содержат перечни предметов соответствующего типа.
# Каждый элемент содержит кортеж, в котором значения означают следующее:
# 0 - название, 1 - атака, 2 - ловкость, 3 - сила, 4 - меткость, 5 - крит, 6 - мастерство
EQUIPMENT_COLLECTION = 'obvious_strong'
RIGHT_HANDS = dict()
RIGHT_HANDS[1] = ('Сильнейший меч', 5000, 0, 0, 0, 0, 0)
RIGHT_HANDS[2] = ('Средний меч', 800, 0, 0, 0, 0, 0)
RIGHT_HANDS[3] = ('Слабый меч', 20, 0, 0, 0, 0, 0)
LEFT_HANDS = dict()
LEFT_HANDS[1] = ('Сильнейший кинжал', 4000, 0, 0, 0, 0, 0)
LEFT_HANDS[2] = ('Слабый кинжал', 10, 0, 0, 0, 0, 0)
GLOVES = dict()
GLOVES[1] = ('Сильнейшие перчатки', 300, 0, 0, 0, 0, 0)
GLOVES[2] = ('Слабые перчатки', 1, 0, 0, 0, 0, 0)
HEADS = dict()
HEADS[1] = ('Сильнейший шлем', 300, 0, 0, 0, 0, 0)
HEADS[2] = ('Слабый шлем', 1, 0, 0, 0, 0, 0)
CHESTS = dict()
CHESTS[1] = ('Сильнейший нагрудник', 300, 0, 0, 0, 0, 0)
CHESTS[2] = ('Слабый нагрудник', 1, 0, 0, 0, 0, 0)
PANTS = dict()
PANTS[1] = ('Сильнейшие поножи', 300, 0, 0, 0, 0, 0)
PANTS[2] = ('Слабые поножи', 1, 0, 0, 0, 0, 0)
BOOTS = dict()
BOOTS[1] = ('Сильнейшие сапоги', 300, 0, 0, 0, 0, 0)
BOOTS[2] = ('Слабые сапоги', 1, 0, 0, 0, 0, 0)
Здесь возможных комбинаций наборов 192 (3 * 2 * 2 * 2 * 2 * 2 * 2). Соответственно, возможных генотипов будет тоже 192.
Главная идея визуализации: представить всё пространство возможных генотипов как прямоугольное поле, где каждый квадратик представляет отдельный генотип. Несложный алгоритм находит два средних делителя числа 192, это 16 и 12:
код этого алгоритма из конструктора класса Stats
# выписать в список все делители числа-суммы генотипов:
list_divisors = list()
current_number = int(self.genotypes_total // 2)
while current_number >= 2:
if self.genotypes_total % current_number == 0:
list_divisors.append(current_number)
current_number -= 1
print('list_divisors:', list_divisors)
# взять индекс примерно из середины полученного списка делителей:
somewhere_in_the_middle = len(list_divisors) // 2
# получить длины сторон будущего прямоугольника:
side_1 = list_divisors[somewhere_in_the_middle]
side_2 = self.genotypes_total / side_1
# определить, какая сторона длиннее, чтобы в будущем прямоугольник "положить" на бок:
self.side_x = int(side_1 if side_1 >= side_2 else side_2)
self.side_y = int(self.genotypes_total / self.side_x)
print('side_x =', self.side_x, 'side_y =', self.side_y)
Получаем область 16х12:

Список возможных генотипов генерируется этим кодом:
# создать список возможных генотипов:
self.list_of_possible_genotypes = list()
# для каждого оружия в правой руке:
for g1 in RIGHT_HANDS:
# для каждого оружия в левой руке:
for g2 in LEFT_HANDS:
# для каждых перчаток:
for g3 in GLOVES:
# для каждого шлема:
for g4 in HEADS:
# для каждого нагрудника:
for g5 in CHESTS:
# для каждых штанов:
for g6 in PANTS:
# для каждой обуви:
for g7 in BOOTS:
current_genotype = str(g1-1)+'-'+str(g2-1)+'-'+str(g3-1)+'-'+str(g4-1)+'-'+str(g5-1)+'-'+str(g6-1)+'-'+str(g7-1)
self.list_of_possible_genotypes.append(current_genotype)
Поэтому квадратики на поле представляют генотипы в таком порядке:

Это важная особенность, ведь, например, генотипы, которые содержат «ген Сильнейшего меча» (голубой уголок) находятся в верхней части поля, а те из них, которые также содержат «ген Сильнейшего кинжала» (синий уголок) — занимают ещё более верхнюю область:

Таким образом, наиболее сильный генотип (0-0-0-0-0-0-0) находится в верхнем левом углу, а наиболее слабый (2-1-1-1-1-1-1) — в противоположном. Это поможет нам при наблюдении за развитием ситуации в динамике, ведь мы будем знать, что в процессе симуляции «доминирующий генофонд» должен смещаться в верхний левый угол поля:

Теперь запустим симуляцию с такими параметрами:
MAX_STAGES = 5
MAX_DAYS_AT_STAGE = 40
SLIDING_FREQUENCY = 1
ROGUES_AT_BEGIN = 8
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1]
HTML_GSQUARE_SIDE = 16
HTML_GSQUARE_MARGIN = 3
То есть 8 разбойников на старте,
-контейнеры с полями (далее — слайды) создаются для каждого дня, 5 стадий по 40 дней. В итоге получим два набора слайдов по 200 штук: "распространённость генотипов" (сине-зелёные цвета) и "победы генотипов" (красные и зелёные цвета). Насыщенность цвета квадратиков зависит от значений.
Открываем сгенерированный HTML-отчёт и видим такую картину для 1-го и 10-го дня:

Итак, в первый день у нас сгенерировалось 8 разбойников, их квадратики до конца симуляции будут отбрасывать тень. Далее видим, что они начали драться, а значит, появляются первые победы, приводящие к размножению. Размножение с большой вероятностью сопряжено с мутациями, поэтому окрашенных квадратиков становится больше.
Заглянем в последующие дни. На 44-й день появился генотип "0-0-0-0-0-0-0" (см. за синей стрелкой). На 59-й день он уже вырвался вперёд по победам (см. за красной стрелкой).

На 137-й день видно, что "0-0-0-0-0-0-0" выбился в лидеры и по количеству появлений в популяции (см. за синей стрелкой). И на слайде последнего дня у него появилась золотая тень, так как он удержал за собой первое место по количеству побед.

Как видим, действительно, естественный отбор смещает «генофонд» популяции влево и вверх, то есть в сторону более сильной экипировки. "Нижеправые" генотипы слабее "верхнелевых", поэтому они исчезают, едва появившись (красный цвет означает отсутствие побед). Более чётко это видно на большем масштабе:

Ну и вердикт в отчёте выдан верный: генотип-победитель — 0-0-0-0-0-0-0:

Графики, полученные при помощи matplotlib, помогут дополнительно оценить происходящее:
1. график "живое население" показывает динамику изменения количества одновременно живущих разбойников;
2. график "родившихся всего" в основном близится к прямой линии, если не начать играться с демографическими параметрами:

3. график "разнообразие генотипов" — обычно быстрый рост сначала, затем замедляется, постепенно приближаясь к максимуму;
4. график "динамика ничьих" — показывает, как с течением времени меняется количество ничьих (это бои, когда в бессмысленной схватке сталкиваются два одинаковых генотипа):

Бывает такое, что популяция «застаивается», когда в ней остаются разбойники с одинаковыми генотипами (на графиках наблюдается: резкий рост количества ничьих, неизменность в численности населения и численности уникальных генотипов).
Застой популяции означает, что вычисление и отрисовка слайдов происходит зря. Чтобы сократить периоды застоя, нужно снизить значение константы MAX_DAYS_AT_STAGE, и будет видно, что застой сократился, а местами вовсе исчез:

ЭТАП 5 — испытываем большие пространства генотипов
Теперь попробуем запустить симуляцию для рассматриваемого в
You must be registered for see links
набора экипировки
You must be registered for see links
чуть с другими параметрами. Здесь значение POSSIBLE_BIRTH_QUANTITIES = [1, 2] означает, что при акте размножения с 50%-ой вероятностью на свет появится либо 1, либо 2 потомка. Это усилит динамику происходящего:MAX_STAGES = 20
MAX_DAYS_AT_STAGE = 50
SLIDING_FREQUENCY = 10
ROGUES_AT_BEGIN = 8
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1, 2]
HTML_GSQUARE_SIDE = 10
HTML_GSQUARE_MARGIN = 3
Здесь паттерн распределения генотипов на слайдах будет иным, ведь наиболее значимая для общего результата экипировка («Меч Мастера») теперь находится в «других местах». Для визуализации этого набора экипировки уже характерно появление ряда «очагов силы» в разных местах, где сила экипировки выше, чем в соседних «районах».

Кстати, этот алгоритм безошибочно определил топовый набор экипировки (3-3-0-0-0-0-1), совпадающий с тем, который определялся комбинаторным алгоритмом с
You must be registered for see links
:
И, наконец, я запустил тест для
You must be registered for see links
, который даёт 18432 комбинации:с такими параметрами
MAX_STAGES = 30
MAX_DAYS_AT_STAGE = 50
SLIDING_FREQUENCY = 100
ROGUES_AT_BEGIN = 20
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1, 2]
HTML_GSQUARE_SIDE = 4
HTML_GSQUARE_MARGIN = 1

В общем, можно продолжать с этим забавляться, но остаётся неизменной тенденция: в ходе симуляции генотипы довольно быстро начинают скапливаться в этих самых «очагах силы». И доминирующий генотип оказывается в одном из самых ярких «очагов».
ЭТАП 6 — а имеет ли это всё смысл?
Если обратиться теперь к практической стороне вопроса, то нужно понять, способен ли этот генетический алгоритм найти правильный ответ ценой меньшего количества боёв, чем простой комбинаторный перебор всех генотипов. Ответ: да, способен. Доказательство под катом:
доказательство эффективности генетического алгоритма
Для этого вернёмся к набору экипировки на 1728 комбинаций.
Комбинаторному алгоритму достаточно подсчитать рейтинг экипировки по одному разу для каждой комбинации, т.е. 1728 раз.
Итак, генетический алгоритм должен найти ответ менее чем за 1728 таких же расчётов. Один «бой» между двумя разбойниками — это сразу 2 расчёта (для каждого из них). Итак, боёв должно быть не больше, чем 1728 / 2 = 864. Поехали.
Подобрал такие параметры:
MAX_STAGES = 8
MAX_DAYS_AT_STAGE = 20
SLIDING_FREQUENCY = 10
ROGUES_AT_BEGIN = 10
WINS_TO_REPRODUCE = 2
DEFEATS_TO_DIE = 2
POSSIBLE_BIRTH_QUANTITIES = [1]
HTML_GSQUARE_SIDE = 10
HTML_GSQUARE_MARGIN = 3
Специально для наглядности выбрал результат, где начальные генотипы расположены подальше от будущего лидера 3-3-0-0-0-0-1:

Отчёт:

Итак, получилось прийти к ответу 3-3-0-0-0-0-1 за 547 боёв. Причём 87 боёв оказались напрасными (ничьи), что составляет 16% бесполезной работы.
На генофондах больших размеров выгода должна быть более ощутима.
P.S. На правильный ответ удаётся выйти даже при ROGUES_AT_BEGIN = 2 и POSSIBLE_BIRTH_QUANTITIES = [1]. Это кажется удивительным, ведь численность популяции ни разу не поднимается выше 2 разбойников. Потому что один проигрывает, другой выигрывает, первый умирает, а второй рождает одного потомка. И родитель начинает состязаться уже с этим потомком. Потомок либо сильнее, либо слабее. И таким образом движется безжалостное колесо отбора между родителем и его же потомком, пока не придёт в лучшую точку (которой сумеет достичь за отведённое время, поэтому это не всегда наилучшая).
Итоги
- Поставленная задача решаема при помощи генетических алгоритмов.
- Визуализация происходящего таким «псевдокартографическим» методом позволяет наблюдать тенденции и динамику в отыскивании эффективных генотипов на всех этапах симуляции.
- При оптимальной комбинации начальных параметров можно добиться того, чтобы генетические алгоритмы использовали меньше ключевых операций, чем это сделает простой перебор всех возможных вариантов (здесь таковой операцией был расчёт силы персонажа в методе calculate_rate класса Rogue, который в иных случаях может быть гораздо более дорогостоящим).
- Разумеется, над этой программой можно ещё экспериментировать и экспериментировать, улучшая эффективность. Например, в какой-то момент начать «банить» явно проигрышные генотипы, не позволяя их владельцам сражаться или даже появляться. Таким образом, будет сужаться воронка «лидеров», где они между собой должны точно определить, кто «сильнейший».
Весь код проекта я выложил на
You must be registered for see links
.Уважаемое сообщество, буду рад обратной связи по этой теме.



