- Регистрация
- 14.05.16
- Сообщения
- 11.398
- Реакции
- 501
- Репутация
- 0
Число пи и случайность цифр после запятой
14 марта в день «3.14» число пи празднует свой день
Важность темы: исследование распределения цифр пи и цифр иррациональных чисел
открывает возможности исследования непрерывных данных в реальном времени,
когда поступающие данные учитываются без пауз на отдельный ввод массива данных
Пробел Просвещения России и СНГ и СССР:
не изучаем логарифм и интеграл в младших классах
и впоследствии считают простейшее якобы трудным
Вдобавок алгоритмы быстрых вычислений в школе не изучаются,
хотя алгоритмы понятны на многих языках программирования
без применения квантовых компьютеров


Понимая паттерны распределений человеческих и натуральных и машинных и фальшивых
реально применять результаты 4-х видов исследований:
1. Создание случайности
2. Преодоление случайности
3. Фальсификация случайности
4. Преодоление фальсификации случайности
Данная тема освещает общедоступный пирамидальный
спектрально интегральный биномиально логарифмический критерий
Используя 55000 цифр числа пи после запятой,
сначала в программе совместимой с Word заменой специальных символов
цифры переведены в столбик и далее в программе совместимой с Excel
цифры разделены на двоичные признаки: малые \ большие и чётные \ нечётные
Результаты: среднее у обоих двоичных распределений: около 0,5
и разделения на двоичные соответствуют вероятности теоретической
Применяется таблица:
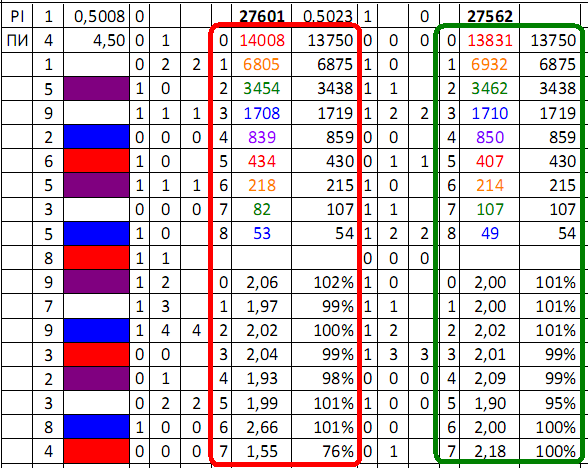
Применены формулы...
Ячейка — Формула — Пояснение
С1 =СРЗНАЧ(D1 55000)
55000)
Среднее значение чисел последовательности
C2 =СРЗНАЧ(B1:B55000)
Среднее значение распределения 1
D1 =ЕСЛИ(B1 Если число меньше среднего, то 0, иначе 1
D2 =ЕСЛИ(B2 Если число меньше ср., то 0, иначе 1 и т.д.
E2 =ЕСЛИ(D2=D1;E1+1;0)
Если одинаковые признаки распределения, то счётчик одинаковых подряд +1,
иначе счётчик обнуляется
F2 =ЕСЛИ(E3=0;E2;" ")
Если счётчик обнулён, фиксируется наибольший счётчик
H2 =СЧЁТЕСЛИ(F$1:F$55000;G2)
Количество признаков 1 подряд и т.д.
H12 =H2/H3
Отношение ближайших количеств признаков
J1 =ЕСЛИ(B1/2=ЦЕЛОЕ(B1/2);0;1)
Если число чётное, то 0, иначе 1
J2 =ЕСЛИ(B2/2=ЦЕЛОЕ(B2/2);0;1)
Если число чётное, то 0, иначе 1 и т.д.
K2 =ЕСЛИ(J2=J1;K1+1;0)
Если одинаковые признаки распределения, то счётчик одинаковых подряд +1,
иначе счётчик обнуляется
L2 =ЕСЛИ(K3=0;K2;" ")
Если счётчик обнулён, фиксируется наибольший счётчик
N2 =СЧЁТЕСЛИ(L$1:L$55000;M2)
Количество признаков 1 подряд и т.д.
N12 =H2/H3
Отношение ближайших количеств признаков
В таблице возможно программировать другие функции контроля
В таблице возможно создавать графики значений любых ячеек
Продолжение таблицы исследует случайные перестановки последовательности

Применены формулы...
Столбец Q – случайные для перестановки: целые до 10^6,
чтобы исключить повтор случайных;
Столбец R – изначально копия столбца B, впоследствии изменяемый;
Столбцы T…AE – то же что столбцы C…N
Ячейка — Формула — Пояснение
Q1 =СЛУЧМЕЖДУ(0;1000000)
Случайное для перестановки
Q2 =СЛУЧМЕЖДУ(0;1000000)
Случайное для перестановки и т.д.
Предварительные выводы: обнаруживается преобладание спектра повторяющихся признаков,
что свойственно для последовательностей природных, например, набрав вручную
3000 цифр, 1-й спектр повторяющихся признаков окажется превышающим теоретическое значение
Используя возможности таблицы для перестановки элементов последовательности и перетасовав,
спектры принимают значения теоретические как были бы синтезированы ГПСЧ и КСГПСЧ
Спектры подчиняются формуле Данилиных: N = LOG(1-c)/LOG(1-p) по принципу:
при С=P=0,5; N = 1 = log0,5/log0,5 = log(1-1/2)/log(1-1/2) = 1
при C=0,25; P=0,5; N = 2 = log0,75/log0,5 = log(1-1/4)/log(1-1/2) = 2 и т.д.
Программа распределения случайных на спектры
количества подряд одинаковых признаков
меньше \ больше и чётный \ нечётный
Практические распределения соответствуют теоретическим
значит случайная последовательность качественная
и возможно изучить паттерны различных последовательностей
Биномиальное Логарифмическое Интегральное Пирамидальное распределение
БЛИП распределение случайных чисел
Binomial Logarithmic Integral Pyramidal Distribution
BLIP distribution of Random numbers
'dablip.bas
RANDOMIZE TIMER
tb = TIMER: s = 0
OPEN "dablip.txt" FOR OUTPUT AS #2
n = VAL(MID$(TIME$, 7, 2))*10 ^ 5
DIM b(n), d(n), e(n), f(n)
DIM j(n), k(n), m(n), p(16), q(16)
LOCATE 1, 1: PRINT " THEORY Average BIG EVEN "
FOR i = 2 TO n-1
b(i) = INT(RND*900)+100: s = s+b(i): m = s/i
IF b(i) < m THEN d(i) = 0 ELSE d(i) = 1
IF (b(i) MOD 2) = 0 THEN j(i) = 0 ELSE j(i) = 1
IF d(i) = d(i-1) THEN e(i) = e(i-1)+1 ELSE e(i) = 0
IF e(i) = 0 THEN f(i) = e(i-1) ELSE f(i) = 12
IF f(i) > 12 THEN f(i) = 12
IF j(i) = j(i-1) THEN k(i) = k(i-1)+1 ELSE k(i) = 0
IF k(i) = 0 THEN m(i) = k(i-1) ELSE m(i) = 12
IF m(i) > 12 THEN m(i) = 12
p(f(i)) = p(f(i))+1: q(m(i)) = q(m(i))+1
IF (i MOD 1000) = 0 THEN LOCATE 3, 1: PRINT i, " from ", n, INT(100*i/n); " %",
NEXT
LOCATE 3, 1: FOR t = 1 TO 12
PRINT INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT
te = TIMER
PRINT: PRINT te-tb; "second", INT(n/(te-tb)); " in second "
PRINT n, " elements ",
PRINT #2, te-tb; "second", INT(n/(te-tb)); " in second "
PRINT #2, n, " elements ",: PRINT #2,
PRINT #2,: PRINT #2, " THEORY Average BIG EVEN ": PRINT #2,
FOR t = 1 TO 12
PRINT #2, INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT
Особенность программы: индексы индексов p(f(i)) & q(m(i))
Думаю у случайных проблемы с чётностью:
слишком резко меняется чётность случайных
Результаты:
40 second 139'555 in second
5'600'000 elements
THEORY Average BIG EVEN
1400000 1400610 1399595 1401625
700000 700026 700122 699931
350000 349716 349508 349925
175000 174823 174892 174755
87500 87424 87564 87285
43750 43837 43931 43744
21875 22028 21983 22074
10937 10850 10865 10835
5468 5481 5496 5466
2734 2755 2732 2778
1367 1388 1396 1380
687 687 687 687
Для самостоятельного изучения:
1. Равномерность каждой из цифр числа пи
1. Методы примерного вычисления числа пи
1. Выучить 8 цифр числа пи после запятой
1. Найти формулы вычисления цифр числа пи
1. Вспомнить формулы длины окружности
14 марта в день «3.14» число пи празднует свой день
Важность темы: исследование распределения цифр пи и цифр иррациональных чисел
открывает возможности исследования непрерывных данных в реальном времени,
когда поступающие данные учитываются без пауз на отдельный ввод массива данных
Пробел Просвещения России и СНГ и СССР:
не изучаем логарифм и интеграл в младших классах
и впоследствии считают простейшее якобы трудным
Вдобавок алгоритмы быстрых вычислений в школе не изучаются,
хотя алгоритмы понятны на многих языках программирования
без применения квантовых компьютеров


Понимая паттерны распределений человеческих и натуральных и машинных и фальшивых
реально применять результаты 4-х видов исследований:
1. Создание случайности
2. Преодоление случайности
3. Фальсификация случайности
4. Преодоление фальсификации случайности
Данная тема освещает общедоступный пирамидальный
спектрально интегральный биномиально логарифмический критерий
Используя 55000 цифр числа пи после запятой,
сначала в программе совместимой с Word заменой специальных символов
цифры переведены в столбик и далее в программе совместимой с Excel
цифры разделены на двоичные признаки: малые \ большие и чётные \ нечётные
Результаты: среднее у обоих двоичных распределений: около 0,5
и разделения на двоичные соответствуют вероятности теоретической
Применяется таблица:

Применены формулы...
Ячейка — Формула — Пояснение
С1 =СРЗНАЧ(D1
Среднее значение чисел последовательности
C2 =СРЗНАЧ(B1:B55000)
Среднее значение распределения 1
D1 =ЕСЛИ(B1 Если число меньше среднего, то 0, иначе 1
D2 =ЕСЛИ(B2 Если число меньше ср., то 0, иначе 1 и т.д.
E2 =ЕСЛИ(D2=D1;E1+1;0)
Если одинаковые признаки распределения, то счётчик одинаковых подряд +1,
иначе счётчик обнуляется
F2 =ЕСЛИ(E3=0;E2;" ")
Если счётчик обнулён, фиксируется наибольший счётчик
H2 =СЧЁТЕСЛИ(F$1:F$55000;G2)
Количество признаков 1 подряд и т.д.
H12 =H2/H3
Отношение ближайших количеств признаков
J1 =ЕСЛИ(B1/2=ЦЕЛОЕ(B1/2);0;1)
Если число чётное, то 0, иначе 1
J2 =ЕСЛИ(B2/2=ЦЕЛОЕ(B2/2);0;1)
Если число чётное, то 0, иначе 1 и т.д.
K2 =ЕСЛИ(J2=J1;K1+1;0)
Если одинаковые признаки распределения, то счётчик одинаковых подряд +1,
иначе счётчик обнуляется
L2 =ЕСЛИ(K3=0;K2;" ")
Если счётчик обнулён, фиксируется наибольший счётчик
N2 =СЧЁТЕСЛИ(L$1:L$55000;M2)
Количество признаков 1 подряд и т.д.
N12 =H2/H3
Отношение ближайших количеств признаков
В таблице возможно программировать другие функции контроля
В таблице возможно создавать графики значений любых ячеек
Продолжение таблицы исследует случайные перестановки последовательности

Применены формулы...
Столбец Q – случайные для перестановки: целые до 10^6,
чтобы исключить повтор случайных;
Столбец R – изначально копия столбца B, впоследствии изменяемый;
Столбцы T…AE – то же что столбцы C…N
Ячейка — Формула — Пояснение
Q1 =СЛУЧМЕЖДУ(0;1000000)
Случайное для перестановки
Q2 =СЛУЧМЕЖДУ(0;1000000)
Случайное для перестановки и т.д.
Предварительные выводы: обнаруживается преобладание спектра повторяющихся признаков,
что свойственно для последовательностей природных, например, набрав вручную
3000 цифр, 1-й спектр повторяющихся признаков окажется превышающим теоретическое значение
Используя возможности таблицы для перестановки элементов последовательности и перетасовав,
спектры принимают значения теоретические как были бы синтезированы ГПСЧ и КСГПСЧ
Спектры подчиняются формуле Данилиных: N = LOG(1-c)/LOG(1-p) по принципу:
при С=P=0,5; N = 1 = log0,5/log0,5 = log(1-1/2)/log(1-1/2) = 1
при C=0,25; P=0,5; N = 2 = log0,75/log0,5 = log(1-1/4)/log(1-1/2) = 2 и т.д.
Программа распределения случайных на спектры
количества подряд одинаковых признаков
меньше \ больше и чётный \ нечётный
Практические распределения соответствуют теоретическим
значит случайная последовательность качественная
и возможно изучить паттерны различных последовательностей
Биномиальное Логарифмическое Интегральное Пирамидальное распределение
БЛИП распределение случайных чисел
Binomial Logarithmic Integral Pyramidal Distribution
BLIP distribution of Random numbers
'dablip.bas
RANDOMIZE TIMER
tb = TIMER: s = 0
OPEN "dablip.txt" FOR OUTPUT AS #2
n = VAL(MID$(TIME$, 7, 2))*10 ^ 5
DIM b(n), d(n), e(n), f(n)
DIM j(n), k(n), m(n), p(16), q(16)
LOCATE 1, 1: PRINT " THEORY Average BIG EVEN "
FOR i = 2 TO n-1
b(i) = INT(RND*900)+100: s = s+b(i): m = s/i
IF b(i) < m THEN d(i) = 0 ELSE d(i) = 1
IF (b(i) MOD 2) = 0 THEN j(i) = 0 ELSE j(i) = 1
IF d(i) = d(i-1) THEN e(i) = e(i-1)+1 ELSE e(i) = 0
IF e(i) = 0 THEN f(i) = e(i-1) ELSE f(i) = 12
IF f(i) > 12 THEN f(i) = 12
IF j(i) = j(i-1) THEN k(i) = k(i-1)+1 ELSE k(i) = 0
IF k(i) = 0 THEN m(i) = k(i-1) ELSE m(i) = 12
IF m(i) > 12 THEN m(i) = 12
p(f(i)) = p(f(i))+1: q(m(i)) = q(m(i))+1
IF (i MOD 1000) = 0 THEN LOCATE 3, 1: PRINT i, " from ", n, INT(100*i/n); " %",
NEXT
LOCATE 3, 1: FOR t = 1 TO 12
PRINT INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT
te = TIMER
PRINT: PRINT te-tb; "second", INT(n/(te-tb)); " in second "
PRINT n, " elements ",
PRINT #2, te-tb; "second", INT(n/(te-tb)); " in second "
PRINT #2, n, " elements ",: PRINT #2,
PRINT #2,: PRINT #2, " THEORY Average BIG EVEN ": PRINT #2,
FOR t = 1 TO 12
PRINT #2, INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT
Особенность программы: индексы индексов p(f(i)) & q(m(i))
Думаю у случайных проблемы с чётностью:
слишком резко меняется чётность случайных
Результаты:
40 second 139'555 in second
5'600'000 elements
THEORY Average BIG EVEN
1400000 1400610 1399595 1401625
700000 700026 700122 699931
350000 349716 349508 349925
175000 174823 174892 174755
87500 87424 87564 87285
43750 43837 43931 43744
21875 22028 21983 22074
10937 10850 10865 10835
5468 5481 5496 5466
2734 2755 2732 2778
1367 1388 1396 1380
687 687 687 687
Для самостоятельного изучения:
1. Равномерность каждой из цифр числа пи
1. Методы примерного вычисления числа пи
1. Выучить 8 цифр числа пи после запятой
1. Найти формулы вычисления цифр числа пи
1. Вспомнить формулы длины окружности

