- Регистрация
- 21.07.20
- Сообщения
- 40.408
- Реакции
- 1
- Репутация
- 0

Прочие статьи цикла
You must be registered for see links
Принятие решений. Пример
You must be registered for see links
скажу, что посмотрел публикации других авторов Хабра по этой теме. Интерес к проблемам имеется, но в теорию влезать никто не желает. Действуют как пионеры первооткрыватели. Это было бы прекрасно, при получении ими новых результатов, достижений, но к этому никто и не стремится. А на деле получается хуже, чем уже известно, не учитывается масса факторов, результаты теории применяются там, где она это делать не рекомендует и вообще не очень серьезно все выглядит, хотя Хабр, как надо понимать к этому и не стремится. Читатели не могут и не должны играть роль фильтра.
Исходное множество альтернатив их измерение и оценивание
Известно, что проблемы поиска решения возникают только в многоальтернативных ситуациях выбора. Для рассмотрения ситуации принятия решения, формулирования конкретной задачи принятия решения (ЗПР), выбора метода ее решения необходимо располагать некоторой исходной информацией об альтернативах, отношением предпочтения.
Покажем в подразделе, какие существуют способы ее получения. Альтернативы обладают многими свойствами (признаками), оказывающими влияние на решение. Например, показатели свойств объектов (вес, объем, твердость, температура и др.) могут быть количественными или качественными.
Пусть некоторое свойство множества альтернатив из Ω выражается числом, т. е. существует отображение ψ: Ω → Е1, где Е1 – множество действительных чисел. Тогда такое свойство характеризуют показателем, а число z = ψ(x) называют значением (оценкой) альтернативы по показателю.
Для проведения оценивания альтернатив необходимо произвести измерение показателей.
Определение. Под измерением показателя некоторого свойства понимается приписывание числовых значений отдельным уровням этого показателя в определенных единицах. При этом важным является выбор единицы измерения.
Так, например, если объем некоторой части емкости сначала измеряется в кубометрах, а затем в литрах, то сущность показателя при этом не изменится; изменится лишь число единиц измерения. Такие показатели свойств допускают масштабирование, умножение или деление значения показателя свойства на постоянную величину.
С другой стороны, имеются свойства, показатели которых не допускают подобного манипулирования с их значениями. Степень нагрева тел характеризуется температурой и измеряется в градусах. Значение этого показателя +10°С и –15°С не позволяют судить о том, во сколько раз больше нагрето тело, имеющее температуру +10°С, чем тело с температурой –15°С
Из этих примеров можно (и важно) сделать вывод о том, что показатели объем и температура относятся к различным типам свойств, над значениями z = ψ(x) которых допустимы или недопустимы определенные преобразования f(z)=f(ψ(x)).
Именно, множество допустимых преобразований f(z) и принимают за основу определения типа шкалы, в которой выполняется измерение показателя некоторого признака (свойства). Выполняя то или иное измерение показателя признака, который выделен исследователем, мы приходим к задаче определения типа шкалы, в которой измерение должно проводиться.
Не решив правильно этой задачи, мы можем допустить некорректное обращение с результатами наблюдений (измерений) при их обработке. Это происходит тогда, когда значения показателей подвергаются преобразованиям, взятым вне множества преобразований допустимых для данного типа шкалы.
Определение. Шкалой измерений называется принятая по соглашению последовательность значений одноименных величин различного размера.
Рассмотрим подробнее основные типы шкал.
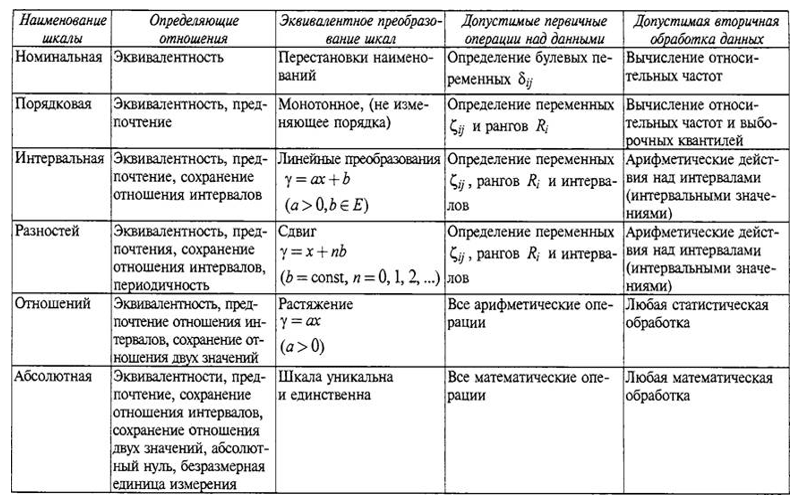
1. Номинальные шкалы. Номинальные шкалы используются тогда, когда исследователь имеет дело с объектами, описываемыми некоторыми признаками. В зависимости от наличия у данного объекта некоторого значения признака или отсутствия такового объект относят к тому или иному классу.
Например, если речь идет о людях, то значение признака (шкала признака образована двумя значениями пола: мужской и женский) позволяет однозначно отнести каждого человека к определенному классу. По этой причине шкалу называют классификационной. Такой признак, как профессия позволяет человека назвать, например, учителем, столяром или как-то иначе в соответствии со значением показателя признака профессия.
Шкала в этом случае образована названиями всех профессий. Очевидно, на этой шкале нуль не обозначен, хотя отсутствие профессии у субъекта допускает его отнесение именно к категории людей без профессии. Названия профессий никак на этой шкале не упорядочены, хотя часто из соображений удобства их располагают при перечислении по алфавиту.
Из этих cоображений такая шкала называется шкалой наименований.
Допустимые преобразования значений в этой шкале — это все взаимно однозначные функции: f(x) ≠ f(y) x ≠ y.
2. Порядковые шкалы. Если изучаемый признак, например, твердость материала, по-разному проявляется у объектов и имеет значения, которые нельзя конкретно измерить, но можно однозначно судить о сравнительной интенсивности его проявления для любых двух объектов, то говорят, что значение признака измеряется в порядковой шкале. Классическим примером такого признака является твердость минералов. Начало отсчета — 0 на шкале не определено.
Значение признака определяется следующим образом. Более твердый минерал рассматриваемой пары оставляет царапину на другом. Все минералы по значениям этого признака могут быть упорядочены так: первый наименее твердый, второй более твердый он оставляет царапину только на первом, третий оставляет царапину на первых двух и т. д.
Отличие порядковой шкалы от номинальной в том, что значения признака удается упорядочить, в то время как значения на номинальной шкале даже упорядочить не удается. Неудобство порядковой шкалы состоит в том, что она не пропорциональная.
Ответить на вопрос насколько или во сколько раз один минерал тверже другого не удается. Допустимые преобразования порядковой шкалы состоят из всех монотонно возрастающих функций, обладающих свойством: x ≥ y => f(x) ≥ f(y).
3. Шкала интервалов (интервальная). отличаются от шкал порядка тем, что для описываемых ими свойств имеют смысл не только соотношения эквивалентности и порядка, но и суммирования интервалов (разностей) между различными количественными проявлениями свойств. Характерный пример — шкала интервалов времени.
Интервалы времени (например, периоды работы, периоды учебы) можно складывать и вычитать, но складывать даты каких-либо событий бессмысленно.
Другой пример, шкала длин (расстояний) — пространственных интервалов определяется путем совмещения нуля линейки с одной точкой, а отсчет делается у другой точки. К этому типу шкал относятся и шкалы температур по Цельсию, Фаренгейту, Реомюру.
В этих шкалах допустимы линейные преобразования, (x — y)/(z -v); x ∓ y; в них применимы процедуры для отыскания математического ожидания, стандартного отклонения, коэффициента асимметрии и смещенных моментов.
4. Шкала разностей(балльная) Шкалы разностей отличаются от шкал порядка тем, что по шкале интервалов можно уже судить не только о том, что размер больше другого, но и на сколько больше в сущности это та же абсолютная шкала, но ее значения сдвинуты на некоторую величину относительно абсолютных значений (x — y) < (z -v); x ∓ y;
5. Шкала отношений. Шкала, для которой множество допустимых преобразований состоит всех преобразований подобия, называется шкалой отношений. На этой шкале фиксируется начало отсчета и для нее допустимо изменение масштаба измерений.
Пусть в этой шкале выполняется измерение длины предмета. При этом можно переходить от измерения в метрах к измерению в сантиметрах, уменьшая единицу измерения в 100 раз. Очевидно, что в этом случае отношение длин L(A) и L(B) двух предметов А и В, измеренных в одинаковых единицах, не изменится при изменении единиц измерения.
Значения показателя признака, измеренные в этой шкале позволяют
отвечать на вопрос во сколько раз интенсивнее признак проявляется у одного предмета, чем у другого. С этой целью необходимо рассмотреть отношение значений L(A)/L(B) = k.
Если отношение больше единицы (k >1), значение показателя признака у первого объекта А в k раз больше чем у В, если k < 1, то значение показателя признака у объекта В в 1/ k раз больше чем у А. Допустимым преобразованием показателя является умножение на целое положительное число и только оно.
6. Абсолютная шкала. Наиболее простой из всех шкал является шкала, допускающая только одно преобразование f(x) = x. Этой ситуации соответствует единственный способ измерения показателя свойства объекта, а именно простой пересчет предметов.
Такая шкала получила название абсолютной шкалы. Когда мы регистрируем объект х, то ничего другое кроме этого объекта нас не интересует. Абсолютная шкала может рассматриваться как частная реализация других некоторых шкал.
Задача принятия решения. Получение матрицы отношений
Перечислим возможные постановки ЗПР, к ним относятся:
— линейное упорядочение альтернатив (верхняя в цепочке лучшая);
— выделение лучшей альтернативы;
— выделение подмножества (неупорядоченного) лучших альтернатив;
— выделение упорядоченного подмножества лучших альтернатив;
— частичное упорядочение альтернатив;
— упорядоченное (частично упорядоченное) разбиение альтернатив;
— неупорядоченное разбиение альтернатив (классификация).
На основе анализа измерений показателей свойств альтернатив в различных шкалах результаты измерений могут быть представлены различными способами [1, 5].
1. Классификационная таблица. Таблица получается при проведении измерений в номинальных шкалах и представляет собой таблицу, строками которой являются: наименование объекта, а столбцами – наименования классов
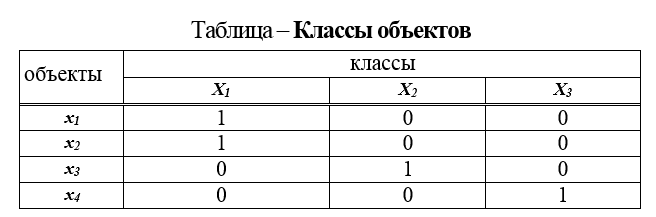
В таблице классов объекты
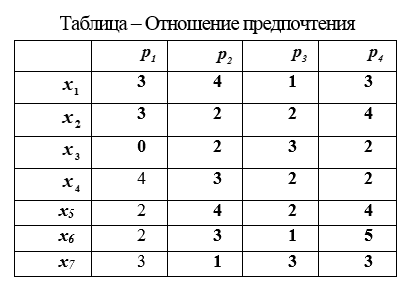
2. Матрица отношения предпочтений. Получается при проведения измерения в порядковых шкалах. Выявить предпочтения на множестве объектов Ω– значит указать множество всех тех пар объектов (х, у) из этого множества для которых объект х предпочтительнее (например, тверже) объекта у. Матрица отношения предпочтений получается следующим образом. (
You must be registered for see links
)Строится
Пример такого отношения предпочтений представлен матрицей ниже
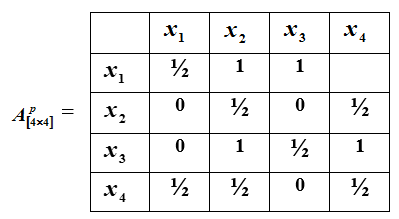
3. Таблица показателей. Получается при проведении измерения в шкале отношений. Выбираются свойства показателей, которых будут измеряться. Производится измерение показателей этих свойств, и результаты измерений записываются в таблицу.
В столбцах
После получения результатов измерений в данных формах представления, нам необходимо произвести отображение результатов в форму отношений, так как мы будем решать ЗПР, опираясь на хорошо разработанный аппарат теории бинарных отношений.
Отображение таблицы предпочтений в матрицу бинарного отношения осуществляется следующим образом:
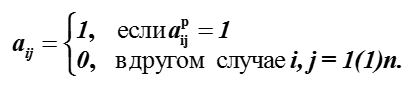
Из матрицы отношения предпочтения
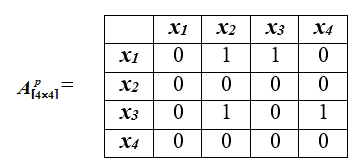
Отображение матрицы показателей в матрицу отношения предпочтения осуществляется следующим образом:
1)число показателей, по которым объект
2) для объекта
3) из условия 1 следует, что те показатели, по которым объект
Однако при выполнении этого условия может оказаться, что по тем показателям, по которым объект
Методы решения задачи принятия решения
Пусть после получения исходных данных мы располагаем отношением R на множестве альтернатив
Отношение R может быть:
1) полным нетранзитивным отношением;
2) отношением частичного порядка;
3) линейным порядком.
Только в случае линейности отношения R, структура предпочтений отвечает поставленной задаче. В этом случае ранжирование альтернатив из множества Ω получается непосредственно, путем построения линейной диаграммы упорядоченного множества. На диаграмме альтернатива
Решение поставленной задачи для полных и транзитивных отношений осуществляется с помощью методов (алгоритма) ранжирования альтернатив, а для частичных порядков с помощью алгоритма линейного доупорядочения. Эти алгоритмы будут рассмотрены в следующих пунктах ниже.
Ранжирование альтернатив. Пусть отношение [Ω, R] – полное и нетранзитивное. Свойство полноты говорит о том, что все альтернативы
Необходимо преобразовать структуру графа отношения так, чтобы были устранены логические противоречия в форме контуров. Если предположить что в отношении R имеется контур
Введем следующее утверждение [1,5].
Пусть В' и В" – два произвольных контура графа вида G[Ω, R], тогда если некоторый элемент
Это предложение предоставляет возможность разбиения множества R на m подмножеств
Итак, задача ранжирования альтернатив множества распадается на два этапа:
1) выделение контуров графа, т.е. разбиение множества Ω на подмножества
2) ранжирование элементов контуров, выделенных на первом этапе.
Алгоритм выделения контуров графа
Для нахождения контуров графа существует простой алгоритм [1]. Пусть
$inline$(Е_{[n×n]}+ А_{[n×n]})^m=(Е_{[n×n]}+А_{[n×n]})^{m+1}$inline$.
Из теории графов известно [10], что каждой системе всех одинаковых строк «установившейся» матрицы соответствует подмножество вершин графа, лежащих в одном контуре. Группируя соответствующие вершины в классы, получим разбиение исходного множества Ω на подмножества
Очевидно, что среди этих подмножеств можно найти такое подмножество
Затем найдем среди оставшихся подмножеств по такому же принципу лучшее подмножество и поставим его на второе место. Эту процедуру будем
продолжать до тех пор, пока все подмножества не займут свои места в ранжировке.
Пусть на множестве Ω задано отношение предпочтения R матрицей

Граф отношения R изображен на рис. Г.
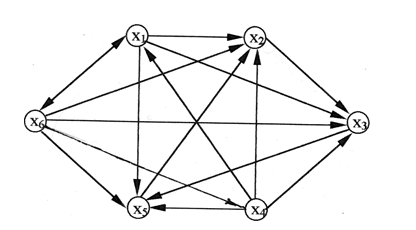
Рис. Г. Граф нетранзитивного отношения R
Для осуществления первого этапа ранжирования элементов множества
необходимо выделить контуры графа G[Ω, R]. Это делается возведением матрицы смежности графа в последовательные степени, пока не выполнится совпадение матриц.
Получаем
Далее последовательно вычисляем возрастающие степени матрицы,
суммируя их с единичной матрицей соответствующей размерности до тех пор пока матрица не перестанет изменяться:
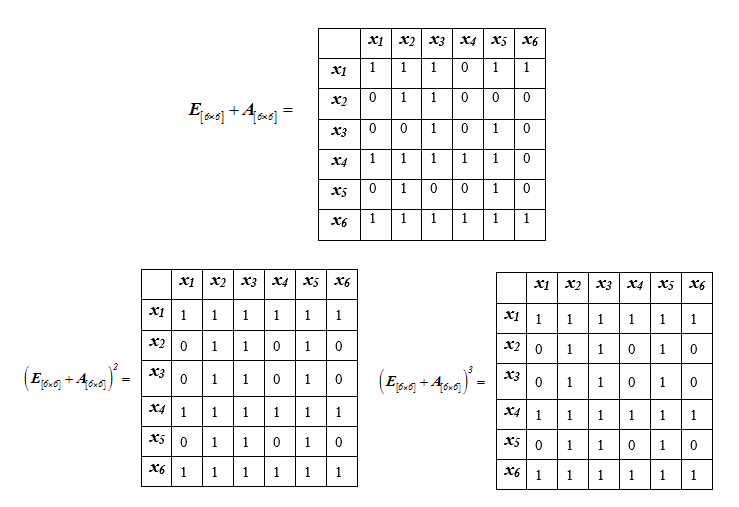
Так как $inline$(Е_{[6×6]}+ А_{[6×6]})^2 =(Е_{[6×6]}+ А_{[6×6]})^3$inline$, можно сделать вывод, что $inline$(Е_{[6×6]}+ А_{[6×6]})^2 = (Е_{[6×6]}+ А_{[6×6]})^k$inline$, при k ≥ 2. Из анализа матрицы
Элементы
Таким образом, мы провели разбиение множества на m=2 класса
Это будет означать превосходство подмножества
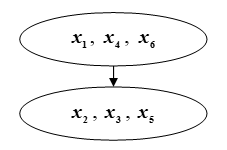
Рис. КК. Ранжирование контуров, выделенных на первом этапе
Алгоритм ранжирования элементов контуров. Возможно, ли упорядочить элементы отношения, лежащие в одном контуре, эквивалентны ли они друг другу или между ними имеют место достаточно тонкие различия, позволяющие их различать? Оказывается такая возможность, как правило, существует [1].
Обозначим через
Пусть
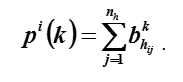
Под относительной силой k-го порядка элемента i понимают дробь
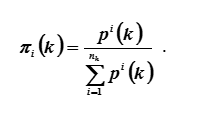
При неограниченном возрастании k (k → ∞), число
Вследствие теоремы Перрона-Фробениуса [1] предел всегда существует. Собственный нормированный вектор матрицы смежности контура совпадет с ее предельным вектором. Следовательно, вектор
может быть найден без вычислений интегрированных сил
где λ – наибольший неотрицательный действительный корень характеристического уравнения
Необходимо отметить, что нормированный собственный вектор неотрицательной неразложимой матрицы не меняется при умножении матрицы на число s > 0, а также при суммировании ее с матрицей вида sE.
Затем элементы контура упорядочиваются по уменьшению значений соответствующих компонентов вектора
Осуществим ранжировку элементов множества
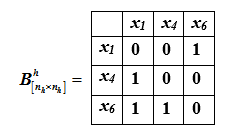
Вектор интегрированных сил 1-го порядка для элементов
Ранжирование элементов
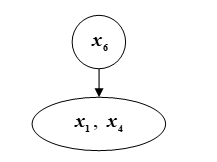
Рис. Р. Ранжирование элементов
Найдем векторы, характеризующие силы 2-го, 3-го, 4-го и 5-го порядков.
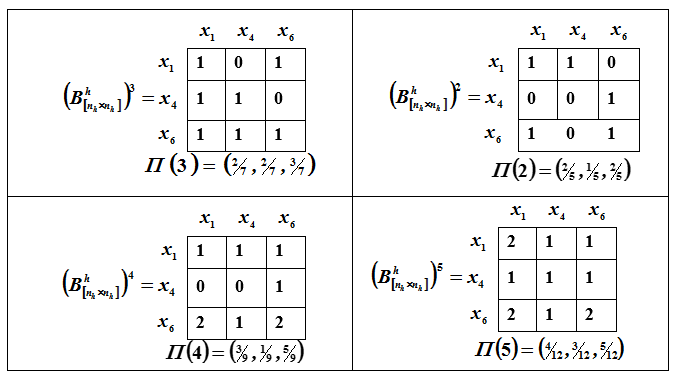
Графическое представление ранжирования изображено на рис. П.
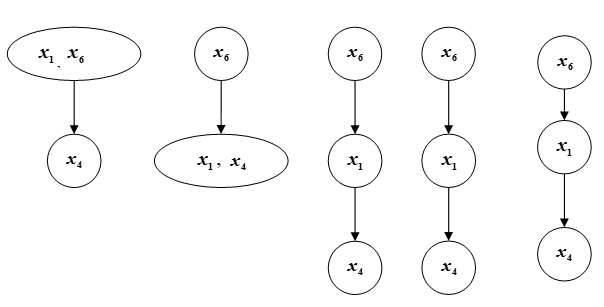

Рис.Ц — Цепь
Осуществив аналогичным образом ранжирование элементов множества В2, получим результаты представленные на рис. П справа.
В результате совмещения ранжировки элементов множества В1 и В2 переходим к окончательному упорядочению элементов множества Ω (рис. Ц).
Линейное доупорядочение строгих частичных порядков
Пусть отношение R (рис. А ниже по тексту), полученное в результате агрегации индивидуальных суждений экспертов является отношением частичного порядка, на множестве Ω. В этом случае Ω– упорядоченное множество. Построение линейного
упорядочения альтернатив представляет собой получение глобальных оценок их «возможностей» в порядковой шкале.
В силу каких-либо причин, некоторые эксперты не могут сравнить определенные пары альтернатив по предпочтительности. В этом случае агрегированное отношение R на множестве Ω не будет линейным порядком. Очевидно, это приводит к задаче линейного доупорядочения альтернатив из Ω. Такое доупорядочение часто возможно многими способами.
Наличие нескольких линейных упорядочений для частичного порядка указывает на то, что имеющегося в структуре «внутреннего порядка недостаточно» для единственного линейного упорядочения. Таким образом, возникает необходимость решения задачи линейного доупорядочения частичных порядков. Пусть R – частичный порядок.
Теорема (Шпильрайн [5, 10]). Всякий порядок R на множестве можно продолжить до линейного порядка на этом множестве.
Следствие из теоремы Шпильрайна: всякое линейное доупорядочение подмножества
Если X – подмножество в Ω, состоящее из несравнимых альтернатив, то всякое линейное упорядочение X может быть продолжено до линейного упорядочения всего множества Ω. При этом порядок R выражается через линейные порядки
В силу теоремы Шпильрайна, на множестве Ω существует нумерация
В общем случае, задача поиска линейных доупорядочений сводится к нахождению всех допустимых нумераций исходного частичного упорядоченного множества. Можно выписать все перестановки элементов, из Ω, которых будет n! и для каждой проверить условие, что «большему» элементу соответствует больший номер. Однако, такой метод отыскания всех доупорядочений очень трудоемкий и не эффективный.
Для упорядоченного множества Ω, с заданным на нем порядком R, элемент х' множества Ω называется максимальным, если не существует строго большего его элемента х, т.е. если x>x' не выполняется ни для какого x є Ω. Элемент x'' называется наибольшим элементом упорядоченного множества [Ω, R], если он больше любого другого элемента х, т.е. для всякого x є Ω, x''>x [5].
Если в упорядоченном множестве имеется наибольший элемент, то он является максимальным элементом. Если в упорядоченном множестве имеется единственный максимальный элемент, то он будет наибольшим элементом. В частично упорядоченном множестве допускается наличие нескольких максимальных элементов.
При всякой нумерации n-элементного множества Ω, номер N приписывается максимальному элементу. Все нумерации множества Ω можно получить, если известны все нумерации всех подмножеств, получающихся из Ω удалением одного из таких максимальных элементов. К каждому подмножеству применим тот же прием [7]. Рассмотрим алгоритм построения всех нумераций упорядоченного множества [Ω, R].
1. Строится вспомогательный граф [β, γR] упорядоченного множества [Ω, R], вершины которого удовлетворяют условиям:
а) являются подмножествами Ω;
б) для любых двух подмножеств X, Y є β верно: (X,Y є γR) тогда, когда
подмножество Y может быть получено из подмножества X удалением одного из его максимальных элементов (рис. А и АА).
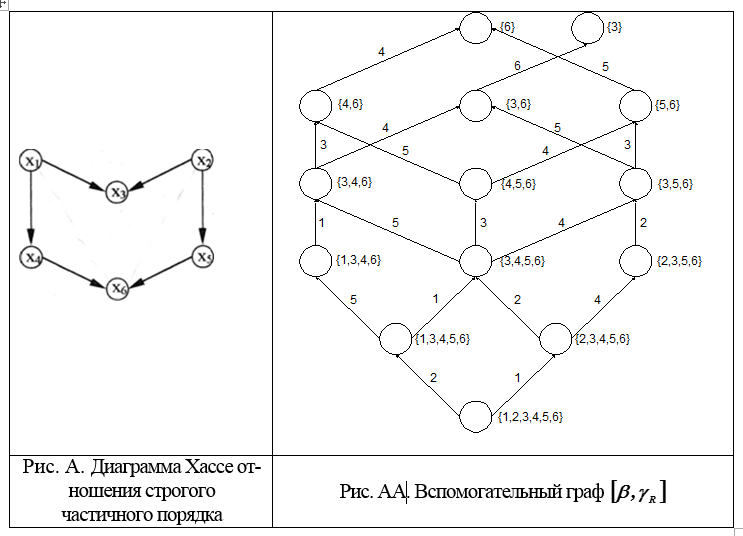
2. Для каждого одноэлементного подмножества множества γR выписываем его единственную нумерацию. Для получения всех нумераций подмножества X необходимо перебрать все смежные с ним подмножества и для каждого такого подмножества продолжить все его нумерации. В итоге будут получены все нумерации множества Ω, т.е. все линейные продолжения порядка R.
Задача заключается в нахождении всех линейных доупорядочений частичного порядка, диаграмма которого представлена на рис. A. В этом отношении нет информации, например, о том, доминирует ли альтернатива
1. Строим вспомогательный граф [β, γR], начинаем с множества
2. Формируем табл. AAA для нахождения всех нумераций подмножеств, являющихся вершинами графа [β, γR]. Заполнение таблицы выполняется построчно сверху вниз. Каждая строка есть нумерация подмножества, записанного в левой колонке таблицы (табл. AAA).
3. При составлении нумерации подмножества X, состоящего из k элементов надо переписать все записанные ранее (для предыдущего подмножества) нумерации подмножеств Y є γR(x) и присвоить номер тому элементу, который дополняет Y до X.
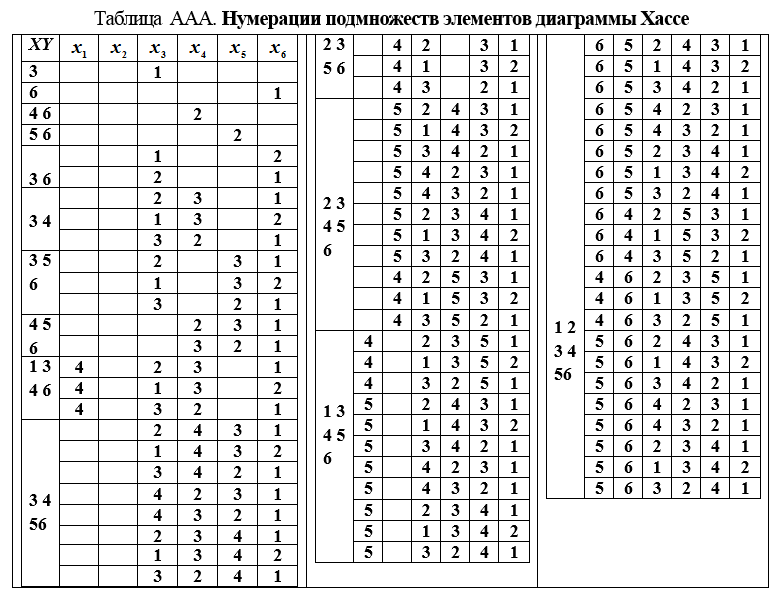
В последнем (нижнем) блоке (табл. AAA) находятся все нумерации линейных доупорядочений множества Ω. Графическое представление этих доупорядочений изображено на рис. AAA.
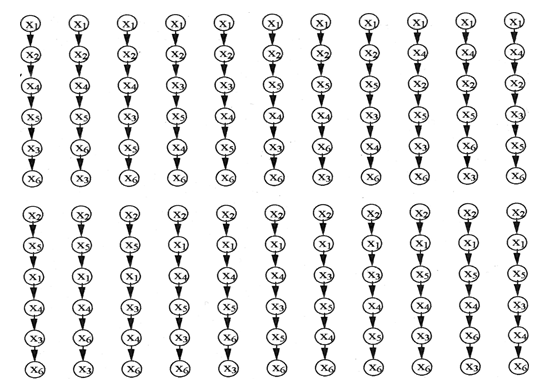
Рис. AAA. Графическое представление доупорядочений
Необходимо отметить, что всего линейных порядков на множестве из 6 элементов 6! или 720, а линейных доупорядочений множества Ω с отношением, заданным графом, изображенным на рис. AA, всего 22. Это также достаточно много для принятия решения.
Существуют ли возможности для сокращения количества таких вариантов? Да существуют.
Для уменьшения числа линейных доупорядочений, необходимо воспользоваться дополнительной информацией.
Дополнительная информация
Пусть [Ω, R] – исходное отношение, тогда дополнительную информацию можно представить в виде отношения δ на множестве Ω, где условие (x,y)є δ, т.е. (x>y) интерпретируется как сообщение о том, что объект х доминирует объект у;
отношение δ можно рассматривать тогда, как множество подобных сообщений информации о доминировании, заданной в виде бинарного отношения δ, возможно два случая при использовании дополнительной информации:
1) граф отношения R∪δ содержит контуры;
2) граф отношения R∪δ не содержит контуров.
В первом случае линейное упорядочение множества Ω с заданным на нем отношением R∪δ производится с помощью алгоритма ранжирования,
рассмотренного ранее.
Во втором случае линейное упорядочение множества Ω с заданным на нем отношением R∪δ производится с помощью алгоритма линейного
доупорядочения, рассмотренного выше. Необходимо отметить, что отношение R∪δ, не содержащее контуров, может быть нетранзитивным и вследствие этого не являться частичным порядком.
Для успешного выхода из этой ситуации необходимо, чтобы дополнительная информация δ и исходное отношение R были заданы в виде диаграмм Хассе, т.е. без явного указания транзитивных связей. Ценность дополнительной информации будет определяться тем, во сколько раз уменьшиться число линейных доупорядочений при ее использовании.
Например, если поступит информация о том, что
Для решения этой задачи для всех пар элементов
Степень ценности дополнительной информации об отношении в этой паре, будет тем выше, чем меньше разность
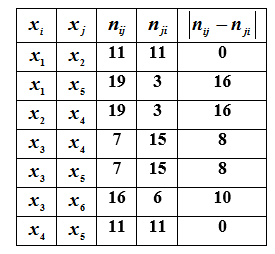
Из анализа таблицы следует, что наиболее полезной будет являться
информация об отношении в парах
Заключение
Формулирование и решение ЗПР возможно только в ситуации множества альтернатив и выбора лучшей из них. Если выбора нет, то следуй путем на котором оказался.
В основе решений, принимаемых ЛПР, лежит его предпочтение, которое описывается отношением предпочтения. Наличие отношения позволяет построить математическую модель для проведения исследований. Неопределенность в предпочтениях устраняется использованием дополнительной информации, которая не является экспертной.
Уделено внимание рассмотрению измерений и оценкам значений показателей свойств объектов. Приведены примеры многообразных шкал, которые часто игнорируются.
Перечислены возможные постановки ЗПР и информация необходимая для их решения.
На конкретном числовом примере показано применение алгебраических методов решения ЗПР, без привлечения статистических выборок и эмпирических методов обработки.
В основе метода лежит результат теоремы о возможности продолжения частичного порядка до линейного (совершенного).
Список использованной литературы
1. Берж К. Теория графов и ее применение. – М.: ИЛ, 1962. – 320 с.
2. Ваулин А. Е. Дискретная математика в задачах компьютерной безопасности. Ч. I. СПб.: ВКА имени А. Ф. Можайского, 2015. – 219 с.
3. Ваулин А. Е. Дискретная математика в задачах компьютерной безопасности.Ч. II. СПб.: ВКА имени А. Ф. Можайского, 2017. – 151 с.
4. Ваулин А. Е. Методы исследования информационных вычислительных комплексов. Вып. 2. – Л.: ВИКИ им. А. Ф. Можайского, 1984. – 129 с.
5. Ваулин А. Е. Методология и методы анализа информационных вычислительных комплексов. Вып.1.– Л.: ВИКИ им. А. Ф. Можайского, 1981. – 117 с.
6. Ваулин А. Е. Методы цифровой обработки данных: дискретные ортогональные преобразования. – СПб.: ВИККИ им. А. Ф. Можайского, 1993. – 106 с.
7. Кузьмин В. Б. Построение групповых решений в пространствах четких и нечетких бинарных отношений. – М.: Наука,1982. – 168 с.
8. Макаров И. М. и др.Теория выбора и принятия решений.– М.: Физматлит, 1982. –328 с.52.
9. Розен В.В. Цель – оптимальность – решение.– М.: Радио и связь,1982.–169 с.
10. Szpilraijn E Sur Textension de l'ordre partiel. — Fundam. math.,1930, vol.16,pp.386-389.

