НОВОСТИ [Перевод] Принятие решений на основе математики: задача о проблеме секретаря

[NewsBot]

You must be registered for see links

Настало время занимательных задач. Представьте, что вы снимаете квартиру в огромном городе. Как свести к минимуму риски при столь значимом выборе, когда вы ничего не знаете о вариантах заранее? На этот вопрос отвечает теория вероятности и задача о проблеме секретаря. Графики, рассуждения, немного кода на Julia — все подробности под катом.


Как теория вероятностей отвечает на вопрос «согласиться или отказать»?

You must be registered for see links

или

You must be registered for see links

в русскоязычной литературе — это известная загадка на тему принятия решений. Речь идет о том, чтобы найти наилучшую стратегию выбора из последовательности, когда вы не знаете, какой вариант лучше. Формулировка задачи звучит так:

Вы менеджер по персоналу и должны нанять лучшего секретаря из

кандидатов. Вы можете собеседовать их одного за другим в случайном порядке. Однако решение о назначении или отказе в назначении на должность должно приниматься сразу после собеседования. Если никто не был принят, выбирается последний кандидат. Какую стратегию вы выберете, чтобы максимально увеличить шансы нанять лучшего кандидата?​

На первый взгляд, эта задача кажется неразрешимой или даже кажется обманом. На самом деле у нее есть элегантное математическое решение. Вытекающая из задачи практическая мудрость обычно теряется на страницах книг по теории вероятностей. Я думаю, что это очень печально, потому что есть много ситуаций, в которых знание оптимальной стратегии выбора среди неизвестных альтернатив может пригодиться. Например:

• Решение снять квартиру в переполненном городе.
• Быстрый поиск старшей карты при перетасовывании колоды.
• Поиск магазина с невысокими ценами без проходов туда и обратно.
• Обязательства перед долгосрочным партнером.

Во всех этих случаях вы не знаете, какие варианты будут следующими. Тем не менее, вы, возможно, захотите принять решение быстро, но также и правильно. Цель этого поста — раскрыть решение проблемы секретаря понятными словами и при необходимости проиллюстрировать решение.

Прежде чем приступать к делу, нужно принять важное решение. Решите для себя, хотите ли вы снова прочитать загадку и подумать о решении самостоятельно. Я настоятельно рекомендую это сделать, потому что это упражнение для ума. Независимо от того, осознаете вы лучшую стратегию или нет. Если вы нетерпеливы, просто прочитайте вывод.​

Случайность? Спасибо, не надо


Проблема секретаря сложна. Невозможно прямо в момент собеседования понять, собеседуете ли вы лучшего кандидата. Вы можете только сравнивать с теми кандидатами, которых уже опросили. Но даже если нынешний кандидат оказался блестящим, самый лучший всегда может прийти сразу после него.

Перед лицом этой полной неопределенности заманчиво довериться удаче. Можно принять произвольное решение: «как бы то ни было, я выбираю первый вариант». Неудивительно, что эта случайная стратегия работает плохо. У вас есть только вероятность

, что первый кандидат будет лучшим. То же самое верно и при выборе всегда последнего претендента или всегда кандидата

ваши шансы всегда

для любого заранее подготовленного варианта.

Случайная стратегия становится все менее пригодной по мере увеличения числа претендентов. Если бы у вас было всего

кандидатов, случайный выбор работал бы только в 33% случаев. При

претендентов шансы случайно выбрать лучшего кандидата составляют жалких 10%. С

это всего 1%. Эти цифры неприемлемы для уважающего себя менеджера по персоналу. Существует ли жизнеспособная стратегия лучше случайного выбора?

Подождать. Подобрать критерии. Опять подождать


В этот момент вы, возможно, поняли, что единственная контролируемая вами переменная — это число людей, которым вы отказали.

Ваша стратегия может состоять только в том, чтобы решить, скольким людям вы хотите отказать, прежде чем начать решать по-настоящему. Сущность подхода — вы хотите подождать достаточно долго, чтобы получить хорошую точку отсчета, а затем выбрать следующего кандидата, подходящего лучше людей, которых вы собеседовали. В количественном выражении эта стратегия формулируется так:

1. Собеседуем R людей и отказываемся нанимать их. Запоминаем лучшего кандидата. Назовем его
   
   .
2. Продолжаем опрашивать следующих кандидатов, пока не найдется первый с оценкой выше
   
   . То есть,
   
   . Выбираем этого кандидата.

Эта стратегия звучит многообещающе, но нужно уточнить деталь: установить, какому количеству людей вы должны отказать.

Когда число

слишком велико, вы можете заложить высокие критерии отбора. Но вы рискуете также сказать «нет» лучшему кандидату. Когда число

слишком мало, у вас будет скучная точка отсчета. Вы, вероятно, выберете неоптимального кандидата. Что нам нужно сделать, так это найти оптимальное значение

количества отказов, учитывая

кандидатов в общей сложности. Чтобы понять это, нам понадобится немного математики.

Однако прежде чем заняться математикой, всегда разумно перепроверить, имеет ли смысл общая идея. Рассмотренную стратегию удобно тестировать в случае

претендентов. Здесь единственная значимое количество людей, которому следует отказать, — это

. В противном случае вы всегда выберете последнего кандидата, если

, или первого, если

, и оба случая будут просто случайной стратегией.

На приведенном ниже рисунке показаны все 6 возможных комбинаций прибытия трех кандидатов вместе с соответствующими результатами стратегии «вызвать первого кандидата, а затем выбрать следующего лучшего (в противном случае последнего)».

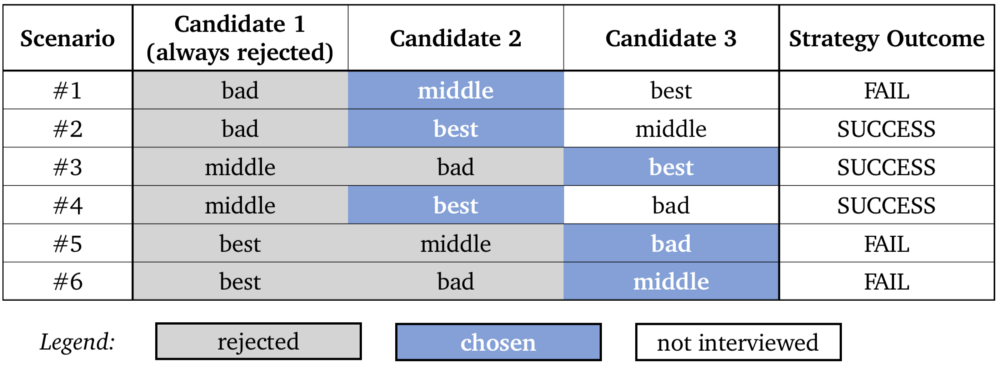
Тестирование оптимальной стратегии остановки с тремя кандидатами.

Стратегия способна выявить лучшего в трех сценариях из шести. То есть мы имеем вероятность успеха

. Это больше, чем

случайной стратегии. Теперь, когда наш метод, кажется, работает, стоит сделать некоторые математические расчеты.

Оптимизация стратегии


Во-первых, нам нужно вычислить вероятность успеха

при выборе лучшего кандидата для некоторого значения

из кандидатов, которым отказали. Вероятность успеха можно рассматривать как сумму вероятностей нахождения наилучшего кандидата в позиции

, где

может состоять из

и общего числа

(т.е. оставшихся кандидатов):

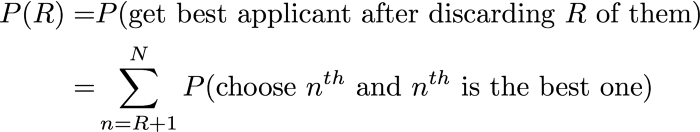
Рассуждение 1: раскладываем вероятность успеха на взаимоисключающие события, где выбирается кандидат n, который также является лучшим.

Напомним, что принятый кандидат — это первый кандидат, набравший наибольшее количество баллов из

отклоненных кандидатов. Однако это не гарантирует, что он также будет лучшим кандидатом в целом. Итак, как рассчитать вероятность того, что выбранный претендент

будет одновременно лучшим? Есть два возможных пути.

Первый способ: рассуждение о втором лучшем кандидате


Выбранный кандидат

, несомненно, также лучший, когда второму лучшему было отказано в самом начале. Это означает, что требования были высокими настолько, чтобы продолжать отвергать кого-либо еще, кроме лучшего кандидата.

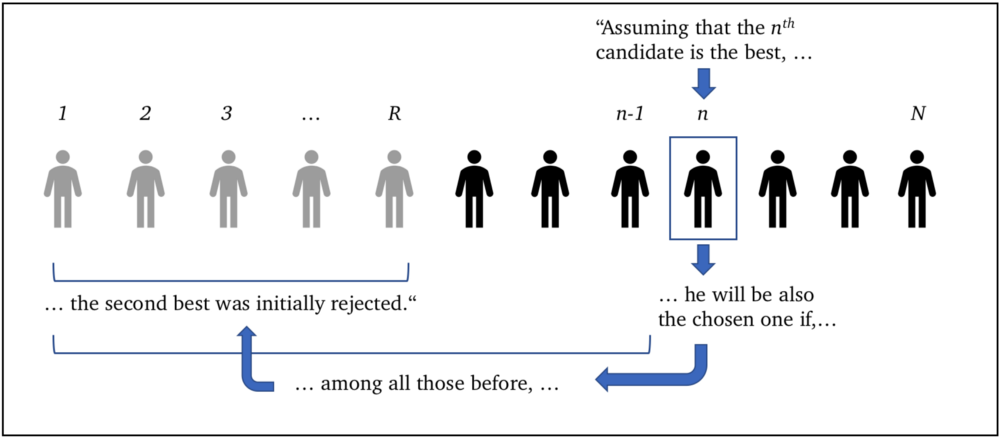
Визуализация рассуждений о позиции второго по значимости кандидата.

На язык математики это переводится так:

Рассуждение 2(а): вычисляем вероятность успеха, установив, что второй лучший кандидат был отброшен среди первых

.

Последнее рассуждение просто выводит из суммы независимые от

факторы. Вот и все. У нас есть формула. Давайте теперь рассмотрим другой способ достижения такого же результата.

Второй способ: рассуждение о количестве зарегистрированных записей


Альтернативный способ потребовать, чтобы был выбран кандидат

и при этом лучший кандидат — это представить себе, что нужно последовательно пройти через всех оставшихся кандидатов от

до

и бросить специальную монету на каждом.

Монета решит, будет ли этот кандидат регистрировать запись о новом рекордном балле. Из-за случайного упорядочения запись происходит с вероятностью

, где

-позиция текущего кандидата. Нам нужен только один максимальный результат для монеты кандидата

, тогда как все остальные монеты должны провалить новый рекорд с вероятностью

.

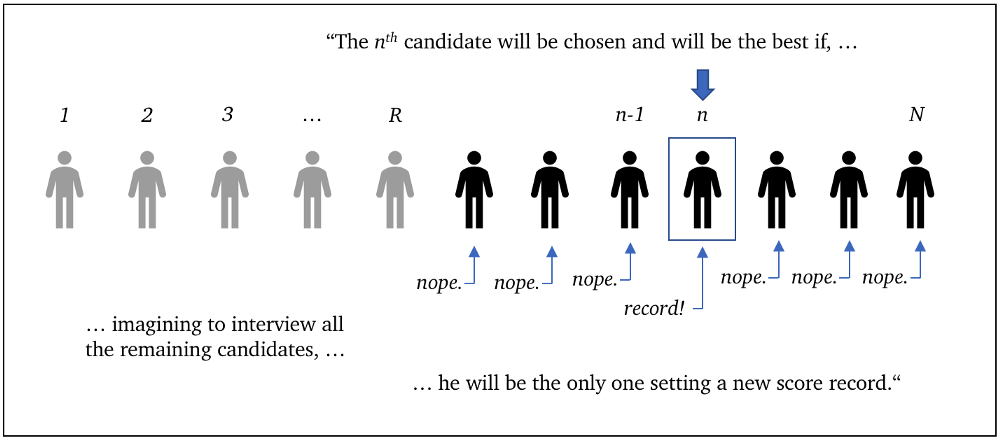
Визуализация рассуждений о наивысших баллах. Математический эквивалент этой идеи:

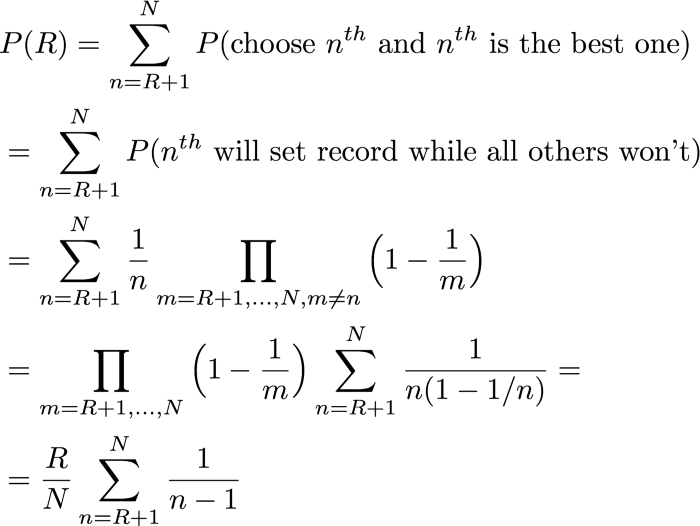
Рассуждение 2(b): вычисляем вероятность успеха, установив, что новый высший балл будет иметь место только один раз до последнего кандидата.

Последняя строка — это просто некоторая алгебраическая манипуляция. Мы проверили, что формула такая же, как и полученная предыдущим способом. В математике это прекрасный момент, когда два разных подхода приводят к одному и тому же результату: часто это весомый признак того, что вы не ошибаетесь.

Оптимальное количество отказов


Теперь, когда у нас есть пуленепробиваемая формула для

, можно легко вычислить значения для заданного числа кандидатов и посмотреть, какое оптимальное число отказов

максимизирует вероятность успеха

. Это легко реализуется, например, на языке Julia:


Ns = collect(1:50) # number of candidates
P(R,N) = R/N*sum([1/(n-1) for n=R+1:N]) # define function P(R)
Ropt = zeros(Int64,length(Ns)) # define vector for R*
Popt = zeros(length(Ns)) # define vector for P(R*)
for N in Ns # optimization loop
Popt[N], Ropt[N] = findmax([P(R,N) for R=1:N])
end


Ниже вы можете увидеть график оптимального

по мере увеличения

и соответствующей вероятности успеха

.

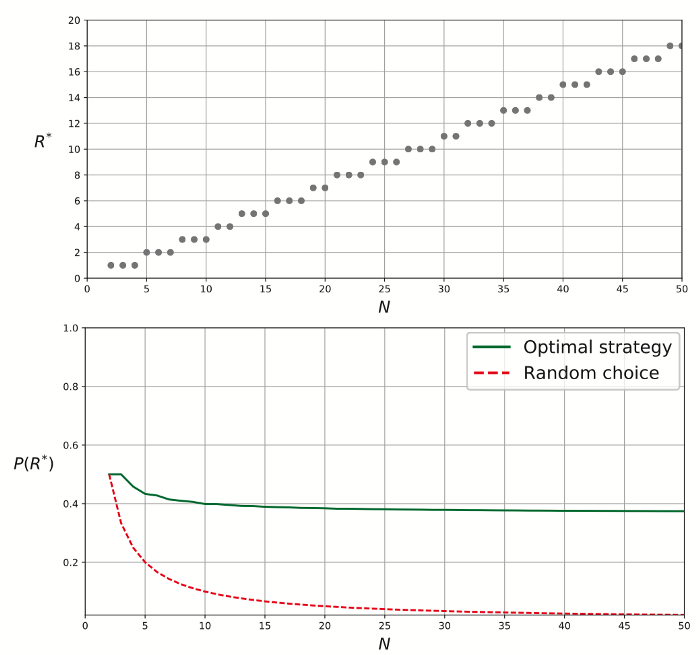
Вверху оптимальное значение отказов, как функция от общего числа кандидатов. Зеленым обозначена вероятность успеха выбора лучшего кандидата, следуя оптимальной стратегии отказов. Красным цветом обозначена низкая вероятность успеха при принятии решения с помощью случайности.

Можно отметить две интересные тенденции. Во-первых, вероятность успеха при оптимальной стратегии не стремится к нулю при больших

, как при случайном выборе. Это поразительно. При оптимальной стратегии вероятность выбора именно лучшего кандидата не уменьшается, когда существует произвольно много кандидатов. Просто подумайте об этом: более вероятно выбрать лучшего кандидата из 100 с оптимальной стратегией, чем преуспеть, выбирая наугад между 3 кандидатами.

Во-вторых, оптимальное значение

следует простой линейной зависимости с

. Можем ли мы извлечь из этого практическое правило?

Да, это закон

.


Закон

получил свое название от асимптотического поведения вероятности успеха: отношение

точно соответствует значению, при котором вероятность успеха

сходится для больших

. Здесь буква

обозначает

You must be registered for see links

, 1/

составляет около 1/2.72≈0.37, как видно из графика.

Точно так же мы наблюдаем, что оптимальное число отказов

растет с

сродни лестнице, совершая прыжок каждые 3 или иногда 2 единицы. Знаете что? Точный наклон снова равен

это означает, что оптимальный

может быть эффективно приближен вычислением

.

Кажущееся магическим значение

может быть явно получено путем приближения второй последней строки на рисунке «Рассуждение 2(b)» для больших

и

, но я опущу это вычисление здесь. Важно отметить, что закон

справедлив и для более общих случаев проблемы секретаря. Например, когда также известно общее число заявителей, но нам дан крайний срок, к которому кандидаты могут подать заявку. Для получения более подробной информации о последнем сценарии вы можете обратиться

You must be registered for see links

.

Заключение


Итак, вы хотите выбрать лучший из нескольких вариантов по принципу «бери или уходи», но ничего не знаете о вариантах? Тогда:

1. Отклоните первые приблизительно
   
   вариантов.
2. Выберите вариант лучше тех, что вы увидели.

You must be registered for see links

Получить востребованную профессию с нуля или Level Up по навыкам и зарплате, можно пройдя онлайн-курсы SkillFactory:

• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links

Eще курсы

• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links
• You must be registered for see links

​