- Регистрация
- 23.09.18
- Сообщения
- 12.347
- Реакции
- 176
- Репутация
- 0
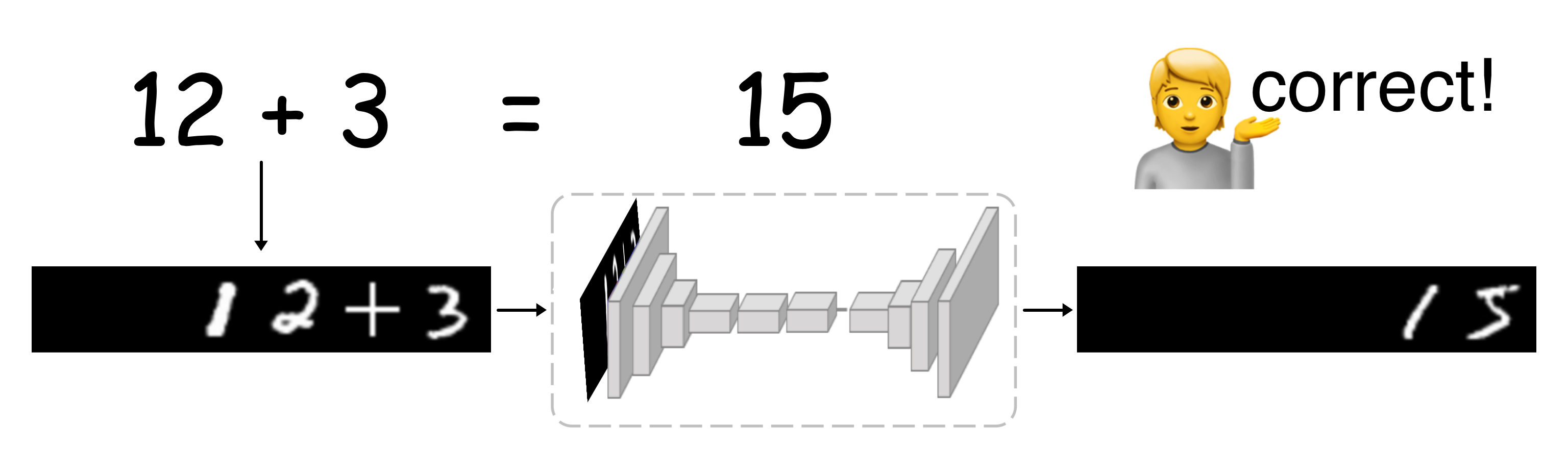
Мы рады представить хабросообществу наш смелый эксперимент: калькулятор, работающий на основе нейросети. Он работает следующим образом: математическое выражение преобразуется в изображение и подается на вход сверточной нейросети, которая генерирует изображение-результат. Полученный калькулятор генерирует изображения правильных ответов, не вычисляя заданное выражение в явном виде.
Работа уже опубликована на
Введение
Генеративно-состязательные сети (Generative Adversarial Networks, GANs) успешно применяются во многих приложениях компьютерного зрения, включая генерацию
Мы следуем тренду развития калькуляторов и представляем нейросетевой калькулятор, принимающий на вход изображение математического выражения и обученный с помощью adversarial-подхода (GAN). Схема работы калькулятора представлена на изображении выше.
Созданный калькулятор поддерживает сложение и вычитание двузначных чисел. Демо находится по адресу
Обзор предыдущих работ
Калькуляторы всегда волновали умы людей. Необходимость складывать и вычитать маленькие (а иногда и большие) числа шла рука об руку с развитием человеческой цивилизации. Существует много трудов, посвящённых этой теме, дальше мы приведём короткий обзор. Опустим часть, связанную с подсчётами на пальцах, отметками на стенах пещер и перейдём сразу же к достижениям индустриальной эпохи.
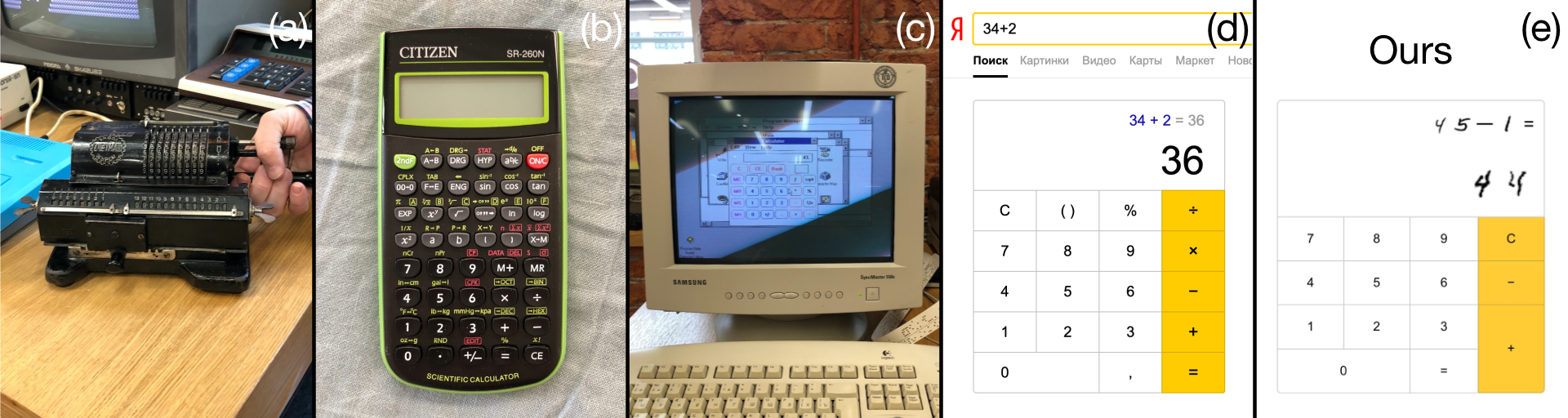
Короткая история калькуляторов: a — механический калькулятор из 1920-х, b — электронный калькулятор из 1980-х, с — калькулятор в Windows 3.x, d — калькулятор в поисковой системе, e — наше решение.
Механический зверь из 1920-х (см. рис. a) поддерживает сложение и вычитание двух девятизначных чисел. Взамен он требует лишь немного внимания и поворотов ручки. Умножение и деление также поддерживаются, но за 10 минут изучения предмета мы так и не поняли, как именно.
Изобретение электронных ламп, транзисторов и микросхем подстегнуло развитие электронных калькуляторов. Мультифункциональный калькулятор, работающий от батарейки (см. рис. b), стал вершиной человеческого творения в вещественном мире. Он сочетает в себе непревзойденную эффективность, удобство использования и функциональность. Идея, что эпоха электронных калькуляторов была лучшим временем человеческой цивилизации, подтверждается многими людьми и агентами. А. Смит сказал: «Поэтому Матрица стала такой. Воссоздан пик вашей цивилизации. Именно вашей цивилизации, ведь когда машины начали думать за вас, возникла наша цивилизация».
В любом случае потом что-то пошло не так и человечество изобрело компьютеры. Сначала для управления требовались перфокарты, потом консоль и, наконец, графический интерфейс.
Высокопроизводительный (относительно карманного калькулятора) компьютер хранит операционную систему в оперативной памяти и выполняет её в бесконечном цикле, видеокарта отрисовывает 60 кадров в секунду, и это всё лишь для того, чтобы отрисовать калькулятор. Монитор светит пикселями вместо того, чтобы использовать солнечный свет. Посмотрите на пример этого безумия (на рис. с): видно, что функциональность калькулятора упрощена, хотя потребление энергии увеличено в сотни раз.
Человечество оступилось в проектировании калькуляторов? Возможно. Нашло ли оно правильный путь? Насколько нам известно, нет. Современный калькулятор — это либо приложение на устройстве, либо веб-страница. Математические выражения — частый тип запросов к поисковым машинам (см. рис. d). Теперь для того, чтобы сложить два числа, требуется не только высокопроизводительное устройство, но и соединение с интернетом (который, без сомнения, очень сложная штука).
Итак, калькуляторы становятся более ресурсоёмкими и менее функциональными. Наш калькулятор (рис. e) — логическое продолжение процесса развития калькуляторов.
Метод
Мы применяем самые современные подходы компьютерного зрения для решения математических выражений. Так как нам не удалось найти в литературе готового датасета для обучения нашей модели, мы собрали собственный.
Мы обнаружили, что существует возможность создания парного датасета математических выражений (например, 5 + 2) и соответствующих им ответов (например, 7). Для сбора данных применялись калькуляторы предыдущих поколений. Для каждой пары выражений и ответов мы генерируем пару изображений, используя случайные числа соответствующих классов из датасета MNIST.
Мы взяли за основу UNet-подобную архитектуру, так как она позволяет принимать картинку на вход и генерировать картинку-результат. Основное отличие нашей модели в том, что мы убрали все skip-connections и добавили несколько полносвязных слоёв в ботлнек-модели. Это сделало модель больше не похожей на UNet. Зато это останавливает сеть от использования частей входной картинки в выходной.
К сожалению, задачу невозможно решить, обучая нейросеть просто с использованием функции потерь L1. Из-за того что изображения ответов собраны из случайных чисел MNIST, сеть сходится к генерации размытых ответов, напоминающих усреднённые числа из MNIST. Для того чтобы поощрять сеть генерировать различное написание чисел, мы предлагаем применять функции потерь
Схема работы калькулятора показана на картинке вверху статьи. Нейросеть принимает отрендерированное выражение и возвращает изображение ответа в форме, которую может интерпретировать человек.
Результаты
Используя процедуру, описанную выше, мы успешно обучили наш нейросетевой калькулятор. Он принимает числа от –99 до 99 и способен складывать и вычитать. Согласно нашему опыту, этого достаточно для покрытия всех повседневных нужд.
Качественные результаты калькулятора показаны на рисунке справа. Результаты, отобранные вручную, показывают идеальное качество работы модели. Также можно

Количественные сравнения нашего калькулятора с другими архитектурами представлены в следующей таблице:
Заключение
С тех пор как мы разработали этот калькулятор, мы показали его многим влиятельным людям в области компьютерного зрения. Некоторые из них посоветовали отправить работу на SIGBOVIK. Мы надеемся, что читатели оценят по достоинству нашу работу, начнут использовать более современный калькулятор и вступят в новую эру вычислений (шутка).
Нельзя не отметить, что нейросеть выучилась простой арифметике, обучаясь только на картинках. Можно было бы упростить задачу, разделив её на три части: распознавание входного изображения, вычисление ответа и генерация изображения ответа. Наша модель работает не так. Несмотря на то, что в ней нет явного арифметического шага, модель всё равно справляется с генерированием правильных ответов.
Важность этого эксперимента в том, чтобы показать, что нейросети способны обобщать даже вот такие логические задачи. Мы не первые, кто проводит подобный эксперимент, есть вот такая
Конечно, в основном Яндекс проводит более практичные исследования. Мы в Лаборатории машинного интеллекта занимаемся генеративными сетями, вот наша последняя
Работа уже опубликована на
You must be registered for see links
и сегодня будет представлена на конференции
You must be registered for see links
в формате аудиозаписи. В этом посте мы поделимся с вами результатами нашего эксперимента. Мотивация и детали реализации также под катом.
Введение
Генеративно-состязательные сети (Generative Adversarial Networks, GANs) успешно применяются во многих приложениях компьютерного зрения, включая генерацию
You must be registered for see links
и
You must be registered for see links
. До настоящего момента было не так много подтверждений, что такие нейросети хороши ещё и в математике.Мы следуем тренду развития калькуляторов и представляем нейросетевой калькулятор, принимающий на вход изображение математического выражения и обученный с помощью adversarial-подхода (GAN). Схема работы калькулятора представлена на изображении выше.
Созданный калькулятор поддерживает сложение и вычитание двузначных чисел. Демо находится по адресу
You must be registered for see links
. Как и положено калькулятору, он считается на устройстве. Для этого используется библиотека TensorFlow.js. Но если она не работает на вашем устройстве, то вы можете воспользоваться
You must be registered for see links
, запущенной на наших серверах.Обзор предыдущих работ
Калькуляторы всегда волновали умы людей. Необходимость складывать и вычитать маленькие (а иногда и большие) числа шла рука об руку с развитием человеческой цивилизации. Существует много трудов, посвящённых этой теме, дальше мы приведём короткий обзор. Опустим часть, связанную с подсчётами на пальцах, отметками на стенах пещер и перейдём сразу же к достижениям индустриальной эпохи.

Короткая история калькуляторов: a — механический калькулятор из 1920-х, b — электронный калькулятор из 1980-х, с — калькулятор в Windows 3.x, d — калькулятор в поисковой системе, e — наше решение.
Механический зверь из 1920-х (см. рис. a) поддерживает сложение и вычитание двух девятизначных чисел. Взамен он требует лишь немного внимания и поворотов ручки. Умножение и деление также поддерживаются, но за 10 минут изучения предмета мы так и не поняли, как именно.
Изобретение электронных ламп, транзисторов и микросхем подстегнуло развитие электронных калькуляторов. Мультифункциональный калькулятор, работающий от батарейки (см. рис. b), стал вершиной человеческого творения в вещественном мире. Он сочетает в себе непревзойденную эффективность, удобство использования и функциональность. Идея, что эпоха электронных калькуляторов была лучшим временем человеческой цивилизации, подтверждается многими людьми и агентами. А. Смит сказал: «Поэтому Матрица стала такой. Воссоздан пик вашей цивилизации. Именно вашей цивилизации, ведь когда машины начали думать за вас, возникла наша цивилизация».
В любом случае потом что-то пошло не так и человечество изобрело компьютеры. Сначала для управления требовались перфокарты, потом консоль и, наконец, графический интерфейс.
Высокопроизводительный (относительно карманного калькулятора) компьютер хранит операционную систему в оперативной памяти и выполняет её в бесконечном цикле, видеокарта отрисовывает 60 кадров в секунду, и это всё лишь для того, чтобы отрисовать калькулятор. Монитор светит пикселями вместо того, чтобы использовать солнечный свет. Посмотрите на пример этого безумия (на рис. с): видно, что функциональность калькулятора упрощена, хотя потребление энергии увеличено в сотни раз.
Человечество оступилось в проектировании калькуляторов? Возможно. Нашло ли оно правильный путь? Насколько нам известно, нет. Современный калькулятор — это либо приложение на устройстве, либо веб-страница. Математические выражения — частый тип запросов к поисковым машинам (см. рис. d). Теперь для того, чтобы сложить два числа, требуется не только высокопроизводительное устройство, но и соединение с интернетом (который, без сомнения, очень сложная штука).
Итак, калькуляторы становятся более ресурсоёмкими и менее функциональными. Наш калькулятор (рис. e) — логическое продолжение процесса развития калькуляторов.
Метод
Мы применяем самые современные подходы компьютерного зрения для решения математических выражений. Так как нам не удалось найти в литературе готового датасета для обучения нашей модели, мы собрали собственный.
Мы обнаружили, что существует возможность создания парного датасета математических выражений (например, 5 + 2) и соответствующих им ответов (например, 7). Для сбора данных применялись калькуляторы предыдущих поколений. Для каждой пары выражений и ответов мы генерируем пару изображений, используя случайные числа соответствующих классов из датасета MNIST.
Мы взяли за основу UNet-подобную архитектуру, так как она позволяет принимать картинку на вход и генерировать картинку-результат. Основное отличие нашей модели в том, что мы убрали все skip-connections и добавили несколько полносвязных слоёв в ботлнек-модели. Это сделало модель больше не похожей на UNet. Зато это останавливает сеть от использования частей входной картинки в выходной.
К сожалению, задачу невозможно решить, обучая нейросеть просто с использованием функции потерь L1. Из-за того что изображения ответов собраны из случайных чисел MNIST, сеть сходится к генерации размытых ответов, напоминающих усреднённые числа из MNIST. Для того чтобы поощрять сеть генерировать различное написание чисел, мы предлагаем применять функции потерь
You must be registered for see links
и
You must be registered for see links
. Для последней мы используем классификационную нейросеть
You must be registered for see links
, обученную распознавать числа из MNIST.Схема работы калькулятора показана на картинке вверху статьи. Нейросеть принимает отрендерированное выражение и возвращает изображение ответа в форме, которую может интерпретировать человек.
Результаты
Используя процедуру, описанную выше, мы успешно обучили наш нейросетевой калькулятор. Он принимает числа от –99 до 99 и способен складывать и вычитать. Согласно нашему опыту, этого достаточно для покрытия всех повседневных нужд.
Качественные результаты калькулятора показаны на рисунке справа. Результаты, отобранные вручную, показывают идеальное качество работы модели. Также можно
You must be registered for see links
.
Количественные сравнения нашего калькулятора с другими архитектурами представлены в следующей таблице:
| Метод | Качество |
|---|---|
Большинство калькуляторов | 100% успеха |
Наш метод | Мы не используем распознавание чисел как часть нашего решения, так как калькулятор предназначен для людей. |
Заключение
С тех пор как мы разработали этот калькулятор, мы показали его многим влиятельным людям в области компьютерного зрения. Некоторые из них посоветовали отправить работу на SIGBOVIK. Мы надеемся, что читатели оценят по достоинству нашу работу, начнут использовать более современный калькулятор и вступят в новую эру вычислений (шутка).
Нельзя не отметить, что нейросеть выучилась простой арифметике, обучаясь только на картинках. Можно было бы упростить задачу, разделив её на три части: распознавание входного изображения, вычисление ответа и генерация изображения ответа. Наша модель работает не так. Несмотря на то, что в ней нет явного арифметического шага, модель всё равно справляется с генерированием правильных ответов.
Важность этого эксперимента в том, чтобы показать, что нейросети способны обобщать даже вот такие логические задачи. Мы не первые, кто проводит подобный эксперимент, есть вот такая
You must be registered for see links
на этот счет. Отличие нашей работы в том, что мы используем различные написания символов и подаем на вход выражение одной картинкой, что усложняет задачу для нейросети. Но она все равно справляется.Конечно, в основном Яндекс проводит более практичные исследования. Мы в Лаборатории машинного интеллекта занимаемся генеративными сетями, вот наша последняя
You must be registered for see links
. Все научные работы Яндекса
You must be registered for see links
.
