- Регистрация
- 21.07.20
- Сообщения
- 40.408
- Реакции
- 1
- Репутация
- 0
В хорошем подмосковном городе есть плохой железнодорожный переезд. В час пик встает не только он, но и соседние перекрестки и дороги. Проезжая в очередной раз, я задался вопросом — какая у него пропускная способность и можно ли что-то изменить?

Для ответа мы немного углубимся в нормативы и теорию транспортных потоков, проанализируем данные GPS и акселерометра с помощью Python и сравним теоретические расчеты с экспериментальными данными.
Содержание
1. Исходные данные
Мы имеет одноколейный железнодорожный переезд с плохим качеством дороги, скорость на котором примерно 10 км/ч. Из подручных средств современный смартфон и ноутбук.
Весь код и данные доступны в формате Jupyter Notebook на моем

Нам понадобятся следующие библиотеки:
import pandas as pd
import numpy as np
import glob
#!pip install utm
import utm
from sklearn.decomposition import PCA
from scipy import interpolate
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(rc={'figure.figsize' 12, 8)})
12, 8)})
import plotly.express as px
# Токен Mapbox для карт в Plotly
mapbox_token = open('mapbox_token', 'r').read()
2. Теория транспортного потока
Для начала определимся с терминами.
Плотность движения $inline$\rho$inline$ — Число автомобилей на 1 км дороги.
$inline$v$inline$ — скорость АТС.
Интенсивность движения $inline$Q(\rho)$inline$ — Количество транспортных средств, проходящие в единицу времени через определенное сечение дороги.
Пропускная способность $inline$P$inline$ — Максимальное число автомобилей, которое может пропустить участок дороги в единицу времени в одном или двух направлениях в рассматриваемых дорожных и погодно-климатических условиях.
Плотность движения и интенсивность связаны формулой:
$$display$$Q = V \cdot \rho$$display$$
Зависимость $inline$Q(\rho)$inline$ часто называют фундаментальной диаграммой.
Так на графике ниже отображены экспериментальные данные «Центра исследования транспортной инфраструктуры» г. Москвы, собранные в течение одного дня в 2005 г. по четырем полосам на участке третьего транспортного кольца от Автозаводской улицы до Варшавского шоссе, и сагрегированные на одну полосу.

Оценка пропускной способности
Основным документом при оценке пропускной способности дорог и их элементов является документ
Для железнодорожных переездов выделен целый раздел, и пропускная способность в разных дорожных условиях рассчитывается по формуле:
$$display$$P_{ж.п.}=P_д \cdot \beta^{ж.п.}_1 \cdot \beta^{ж.п.}_2 \cdot \beta^{ж.п.}_3 \cdot \beta^{ж.п.}_4 \cdot \beta^{ж.п.}_5,$$display$$
где $inline$\beta^{ж.п.}_1,\beta^{ж.п.}_2,\beta^{ж.п.}_3,\beta^{ж.п.}_4,\beta^{ж.п.}_5$inline$ — коэффициенты снижения пропускной способности, учитывающие состав движения, характеристики железнодорожных переездов и дорожные условия в зоне переезда, которые определяются по приведенным таблицам.
Рассчитаем пропускную способность, исходя из наших условий:
$$display$$P_{ж.п.}=1500 \cdot 0.93 \cdot 0.66 \cdot 0.8 \cdot 1 \cdot 1 = 736.56 авт./ч = 12.3 авт./мин$$display$$
Мы получили теоретическую оценку, теперь перейдем к тому, что есть на самом деле.
В реальных условиях я использовал 2 метода оценки пропускной способности:
В качестве функционала можно использовать простые модели:
$inline$\rho(v)=\frac{1}{d(v)}$inline$,
$inline$d(v)= L+ c_1 v+ c_2 v^2$inline$,
где $inline$d(v)$inline$ – среднее (безопасное) расстояние между АТС, $inline$L$inline$ – средняя длина АТС, $inline$c_1$inline$ – время, характеризующее реакцию водителя, $inline$c_2$inline$ — коэффициент пропорциональности тормозному пути. При нормальных условиях (сухой асфальт): $inline$L=5.7 м, c_1=0.504 c, c_2=0.0285 с^2/м$inline$.
$inline$\rho= \rho_{max} (1 - \frac{v}{v_{max}})$inline$,
где $inline$\rho_{max}$inline$ — максимальная плотность потока (при отсутствии движения), $inline$v_{max}$inline$ — максимальная (желаемая) скорость движения АТС (при пустой дороге). Эти данные можно взять из того же ОДМ 218.2.020-2012 — $inline$\rho_{max} = 85 авт./км, v_{max}=60 км/ч$inline$
Код для графиков
# Загрузка данных для Диаграммы уравнения потока
diagram1 = pd.read_csv('Диаграмма уравнения потока.csv', sep=';', header=None, names=['P', 'V'], decimal=',')
diagram1_func = interpolate.interp1d(diagram1['P'], diagram1['V'], kind='cubic')
diagram1_xnew = np.arange(diagram1['P'].min(), diagram1['P'].max())
# Загрузка данных для Фундаментальной диаграммы
diagram2 = pd.read_csv('Фундаментальная диаграмма.csv', sep=';', header=None, names=['P', 'Q'], decimal=',')
diagram2_func = interpolate.interp1d(diagram2['P'], diagram2['Q'], kind='cubic')
diagram2_xnew = np.arange(diagram2['P'].min(), diagram2['P'].max())
def density_Tanaka(V):
# Функция плотности для модели Танака
V = V * 1000 / 60 / 60 # переводим км/ч в м/с
L = 5.7 # м
c1 = 0.504 # с
c2 = 0.0285 #с**2/м
return 1000 / (L + c1 * V + c2 * V**2) # авт./км
def density_Grindshilds(V):
# Функция плотности для модели Гриндшилдса
pmax = 85 # авт./км
vmax = 60 # км/ч
return pmax * (1 - V / vmax) # авт./км
# Построение графиков
V = np.arange(1, 80) # км/ч
V1 = np.arange(1, 61) # км/ч
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))
ax1.plot(density_Tanaka(V), V, label="Модель Танака")
ax1.plot(density_Grindshilds(V1), V1, label="Модель Гриндшилдса")
ax1.plot(diagram1_xnew, diagram1_func(diagram1_xnew), label="Экспер. данные ТТК")
ax1.set_xlabel(r'Плотность $\rho$, авт/км')
ax1.set_ylabel(r'Скорость $V$, км/ч')
ax1.legend()
ax2.plot(density_Tanaka(V), density_Tanaka(V) * V, label="Модель Танака")
ax2.plot(density_Grindshilds(V1), density_Grindshilds(V1) * V1, label="Модель Гриндшилдса")
ax2.plot(diagram2_xnew, diagram2_func(diagram2_xnew), label="Экспер. данные ТТК")
ax2.set_xlabel(r'Плотность $\rho$, авт/км')
ax2.set_ylabel(r'Интенсивность $Q$, авт/ч')
ax2.legend()
plt.show()
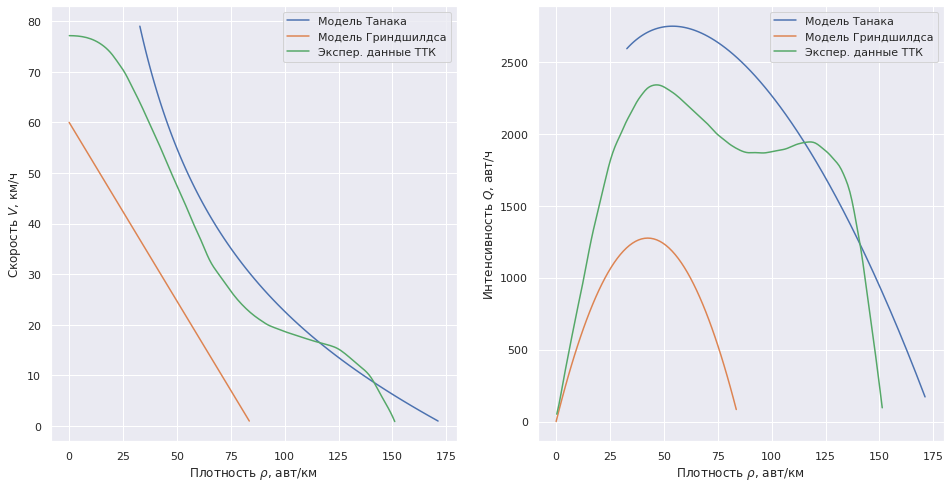
Модель Гриндшилдса с исходными данными для переезда существенно занижает интенсивность по сравнению с экспериментальными данными для обычной дороги. Давайте сравним эту модель с реальностью.
3. Сбор и анализ данных
3.1 Ручной подсчет интенсивности движения
Я не стал усложнять и применять нейронные сети для распознавания машин, а просто написал кейлогер с сохранением времени и нажатой клавиши. Чтобы после каждого нажатия не вводить Enter, код немного усложнился:
Код кейлогера
%%writefile "key-logger.py"
import pandas as pd
import time
import datetime
class _GetchUnix:
# from
def __init__(self):
import tty, sys
def __call__(self):
import sys, tty, termios
fd = sys.stdin.fileno()
old_settings = termios.tcgetattr(fd)
try:
tty.setraw(sys.stdin.fileno())
ch = sys.stdin.read(1)
finally:
termios.tcsetattr(fd, termios.TCSADRAIN, old_settings)
return ch
def logging():
path = 'logs/keylog/'
filename = f"{time.strftime('%Y-%m-%d %H-%M-%S')}.csv"
path_to_file = path + filename
db = []
getch = _GetchUnix()
print('Процесс...')
while True:
key = getch()
if key == 'c':
break
else:
db.append((datetime.datetime.now(), key))
df = pd.DataFrame(db, columns=['time', 'click'])
print(df)
df.to_csv(path_to_file, index=False)
print(f"\nSaved to {filename}")
if __name__ == "__main__":
logging()
Пришлось посидеть возле переезда 20 минут и внимательно смотреть за потоком. Я записал 2 периода сразу после проезда поезда, т. е. при загрузке переезда на 100%:
files = glob.glob('logs/keylog/*.csv')
keylogger_data = []
print(f'Количество файлов - {len(files)} шт.')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'])
keylogger_data.append(df)
keylogger_data = pd.concat(keylogger_data, ignore_index=True)
keylogger_data.head()
Клавиша "a" — машина проехала через переезд из города, клавиша 'd' — в город.
Сагрегируем данные по минутам и направлению:
keylogger_data['time'] = keylogger_data['time'].astype('datetime64[m]')
keylogger_per_min = keylogger_data.groupby(['click', 'time'], as_index=False).size().reset_index().rename(columns={0:'size'})
keylogger_per_min.head()
sns.catplot(x='click', y='size', kind="box", data=keylogger_per_min);
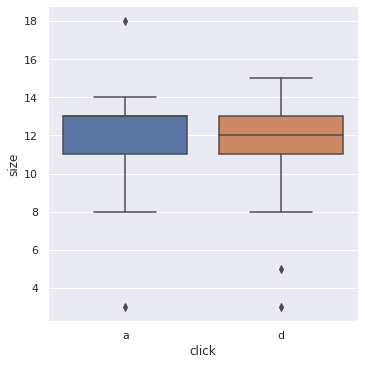
print(f"Средняя пропускная способность: {keylogger_per_min['size'].mean():.1f} авт./мин \
или {keylogger_per_min['size'].mean() * 60:.1f} авт./ч")
Средняя пропускная способность: 11.7 авт./мин или 700.0 авт./ч
Экспериментальная интенсивность почти соответствуют расчетной с неудовлетворительным состоянием переезда.
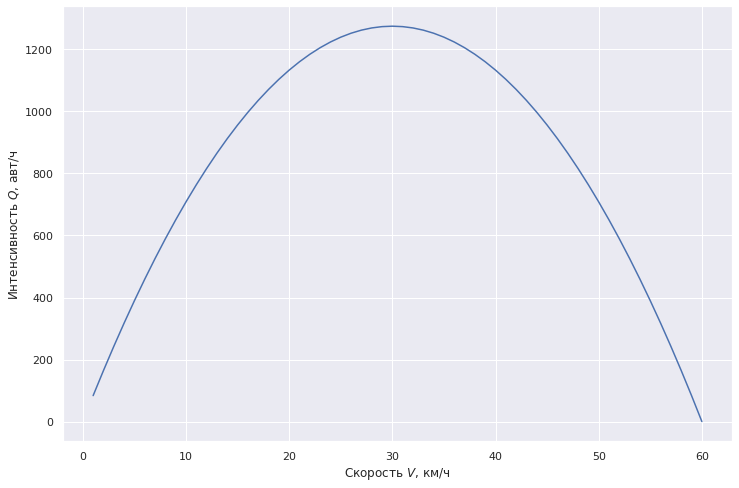
Вспомним нашу модель Гриндшилдса — интенсивности в 700 авт./ч соответствует скорость около 10 км/ч (о 50 км/ч речи не идет) — по ощущения при переезде это так и есть.
plt.plot(V1, density_Grindshilds(V1)*V1, label="Модель Гриндшилдса")
plt.xlabel(r'Скорость $V$, км/ч')
plt.ylabel(r'Интенсивность $Q$, авт/ч')
plt.show()
3.2 Измерение средней скорости на переезде
Для измерения скорости я использовал приложение для Android GPSLogger с сохранением трекинга в csv файлы. В процессе написания статьи возникла идея посмотреть на данные акселерометра (линейного ускорения) с привязкой данных GPS — с этим отлично справилось приложение Physics Toolbox Suite.
За всё время у меня набралось около 50 проходов переезда. Данные записывались и при нулевом трафике и в пробках — я старался проезжать переезд со скоростью потока.
Загрузим все данные, при этом сразу добавим информацию о направлении движения — это понадобится в дальнейшем для графиков.
Данные приложения GPSLogger
Приложение GPSLogger сохраняет много информации, но нам потребуется только:
files = glob.glob('logs/gps/*.csv')
gpslogger_data = []
print(f'Количество файлов с данными GPS - {len(files)} шт.')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'], index_col='time')
if df.iloc[10, 1] < df.iloc[-1, 1]:
df['direction'] = 0 # в город
else:
df['direction'] = 1 # из города
gpslogger_data.append(df)
gpslogger_data = pd.concat(gpslogger_data)
gpslogger_data.head()
gps_1 = gpslogger_data[['lat', 'lon', 'speed', 'direction']]
Количество файлов с данными GPS — 37 шт.
Данные приложения Physics Toolbox Suite:
files = glob.glob('logs/gps_accel/*.csv')
print(f'Количество файлов с данными акселерометра - {len(files)} шт.')
pts_data = []
for filename in files:
df = pd.read_csv(filename, sep=';',decimal=',')
df['time'] = filename[-22:-12] + '-' + df['time']
if df.iloc[10, 5] < df.iloc[-1, 5]:
df['direction'] = 0 # в город
else:
df['direction'] = 1 # из города
pts_data.append(df)
pts_data = pd.concat(pts_data)
pts_data.head()
Количество файлов с данными акселерометра — 14 шт.
Данные содержат некорректные записи с нулевой широтой, долготой — почистим:
pts_data = pts_data.query('Latitude != 0.')
Приложение Physics Toolbox Suite записывает данные с максимальной частотой для акселерометра 400 Гц, но датчик GPS работает с частотой 1 Гц, поэтому разделим данные по датчикам:
pts_data['time'] = pd.to_datetime(pts_data['time'], format='%Y-%m-%d-%H:%M:%S:%f')
pts_data = pts_data.rename(columns={'Latitude':'lat', 'Longitude':'lon', 'Speed (m/s)':'speed'})
Данные акселерометра:
accel_data = pts_data[['time', 'lat', 'lon', 'ax', 'ay', 'az', 'direction']].copy()
accel_data = accel_data.set_index('time')
accel_data['direction'] = accel_data['direction'].map({1.: 'Из города', 0.: 'В город'})
accel_data.head()
Данные GPS:
gps_2 = pts_data[['time', 'lat', 'lon', 'speed', 'direction']].copy()
gps_2 = gps_2.set_index('time')
gps_2 = gps_2.resample('S').mean()
gps_2 = gps_2.dropna(how='all')
gps_2.head()
Объединим все GPS данные:
gps_data = gps_1.append(gps_2, ignore_index=True)
gps_data['direction'] = gps_data['direction'].map({1.: 'Из города', 0.: 'В город'})
gps_data.head()
3.2.1 Визуализация на карте
Визуализируем данные на карте с помощью библиотеки Plotly:
fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()

3.2.2 Визуализация профиля переезда
Чтобы построить график продольного сечения переезда нужно выполнить два преобразования:
В сервисах онлайн карт обычно используется проекция Web Mercator, которая имеет один недостаток — это сильное искажение расстояний, именно поэтому Гренландия на картах выглядит больше Африки, хотя на самом деле меньше в несколько раз.
Для геодезических и картографических работ применяются проекции, основанные на поперечной проекции Меркатора. В России и многих других странах применяется проекция Гаусса — Крюгера, в США — универсальная поперечная проекция Меркатора (UTM).
Проекция Web-Mercator
Проекция UTM
Для преобразования в UTM для Python есть простое решение
gps_data['xs'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
gps_data['ys'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
gps_data['speed_kmh'] = gps_data.speed / 1000 * 60 * 60
Оставим данные только вокруг переезда в радиусе 50 метров:
# Координаты переезда
lat0 = 56.35205
lon0 = 37.51792
xc, yc, _, _ = utm.from_latlon(lat0, lon0)
r = 50
gps_data = gps_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')
fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()
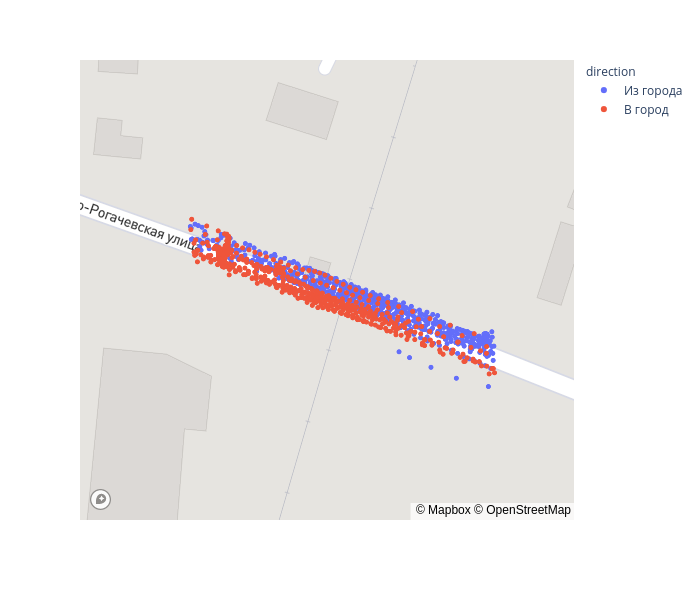
Теперь спроецируем точки на ось дороги. Это по сути задача понижения размерности с 2d в 1d, которая решается методом главных компонент (PCA).
Мы можем поступить 2 способами — вручную вычислить матрицу поворота и взять одну компоненту или довериться реализации scikit-learn. Для простоты выберем Sklearn:
pca = PCA(n_components=1).fit(gps_data[['xs', 'ys']])
gps_data['xs_transform'] = pca.transform(gps_data[['xs', 'ys']])
sns.relplot(x='xs_transform', y='speed_kmh', data=gps_data, aspect=2.5, hue='direction');

В большинстве случаев после переезда скорость возрастает. По графику можно выделить границы переезда — это примерно интервал [-5, 25]. Для уточнения посмотрим на данные с акселерометра.
accel_data['xs'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
accel_data['ys'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
accel_data = accel_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')
accel_data['xs_transform'] = pca.transform(accel_data[['xs', 'ys']])
Оси акселерометра в Android располагаются следующим образом:
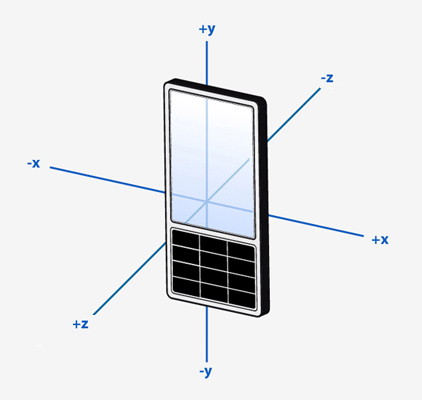
При записи данных телефон всегда лежал по ходу движения (ось Y). Посмотрим на графики отдельно по осям:
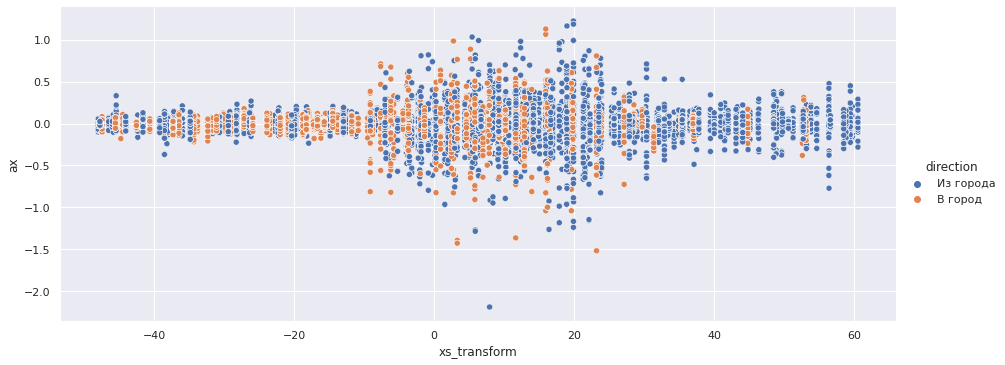
sns.relplot(x='xs_transform', y='ax', data=accel_data, aspect=2.5, hue='direction');
sns.relplot(x='xs_transform', y='ay', data=accel_data, aspect=2.5, hue='direction');
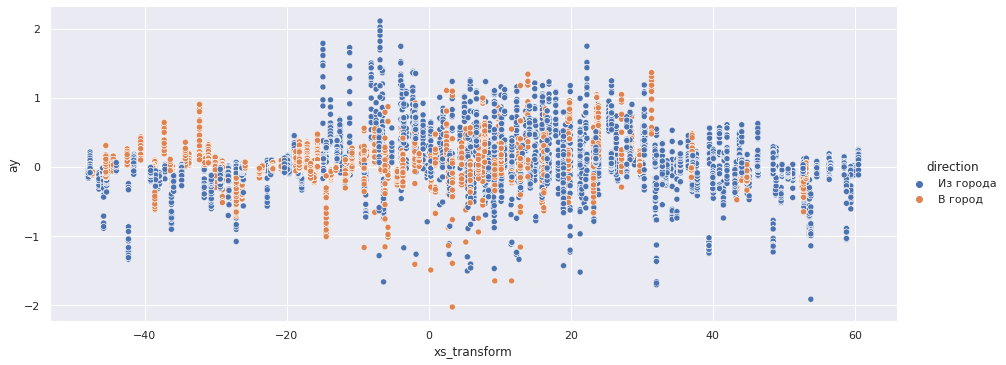
sns.relplot(x='xs_transform', y='az', data=accel_data, aspect=2.5, hue='direction');

Увеличим масштаб по оси Z:
sns.relplot(x='xs_transform', y='az', data=accel_data.query('-20 < xs_transform < 40'), aspect=2.5, hue='direction');
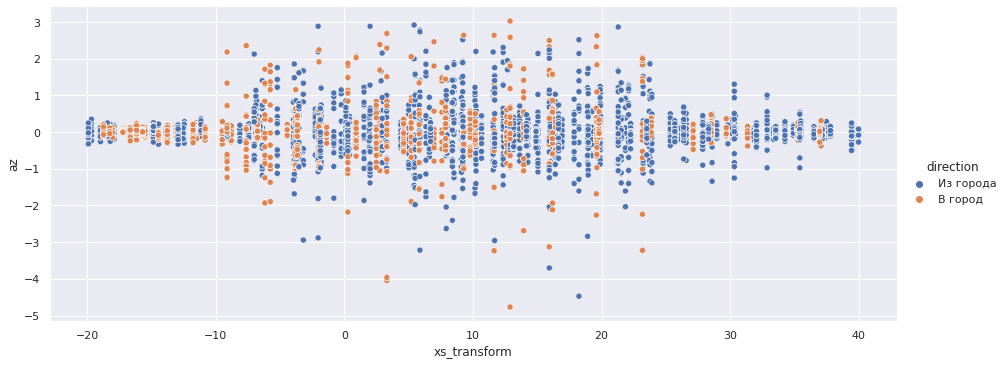
По осям X и Z четко определяются границы переезда — интервал [-10, 25] с центром в точке 7.5.
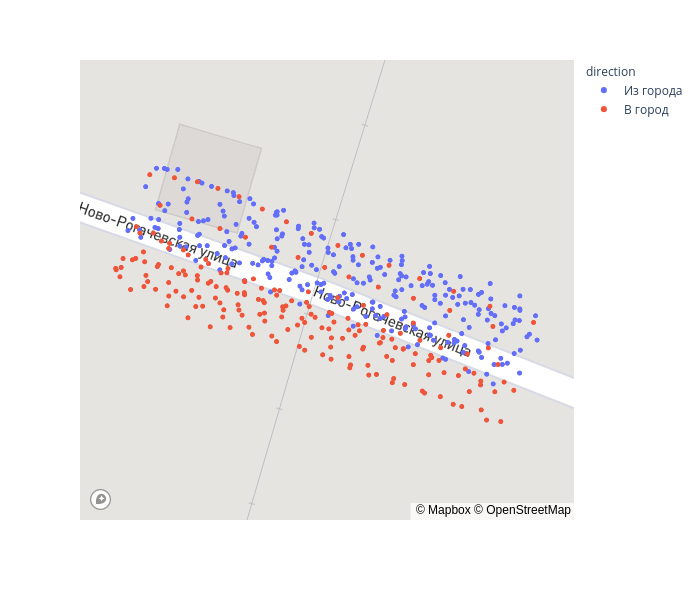
cross = gps_data.query('-10 < xs_transform < 25')
fig = px.scatter_mapbox(cross, lat="lat", lon="lon", color='direction', zoom=19, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()
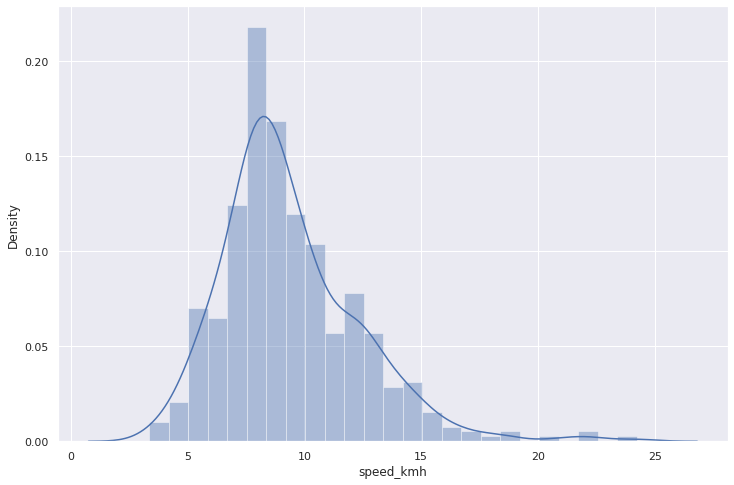
Теперь посмотрим как распределена скорость на переезде:
mean_v = cross.speed_kmh.mean()
print(f"Средняя скорость на переезде - {mean_v:.2} км/ч")
sns.distplot(cross.speed_kmh);
Средняя скорость на переезде — 9.4 км/ч
Округлим координаты до метра и построим еще немного красивых графиков:
base = 1
gps_data['xs_transform_round'] = gps_data['xs_transform'].apply(lambda x: base * round(x / base))
accel_data['xs_transform_round'] = accel_data['xs_transform'].apply(lambda x: base * round(x / base))
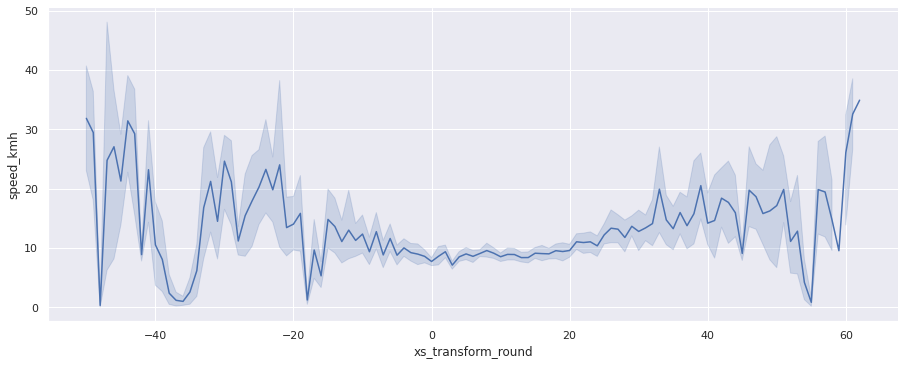
sns.relplot(x='xs_transform_round', y='speed_kmh', data=gps_data, kind="line", aspect=2.5);
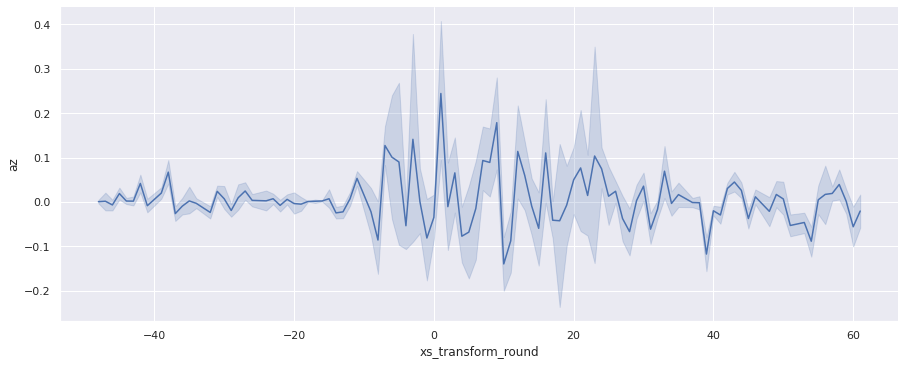
sns.relplot(x='xs_transform_round', y='az', data=accel_data, kind="line", aspect=2.5);
3.3 Оценка плотности
Для расчета пропускной способности используем две модели для плотности:
gps_data['flow_Tanaka'] = density_Tanaka(gps_data.speed_kmh) * gps_data.speed_kmh
gps_data['flow_Grindshilds'] = density_Grindshilds(gps_data.speed_kmh) * gps_data.speed_kmh
sns.relplot(x='xs_transform_round', y='flow_Grindshilds', data=gps_data, aspect=2.5, kind='line', hue='direction');
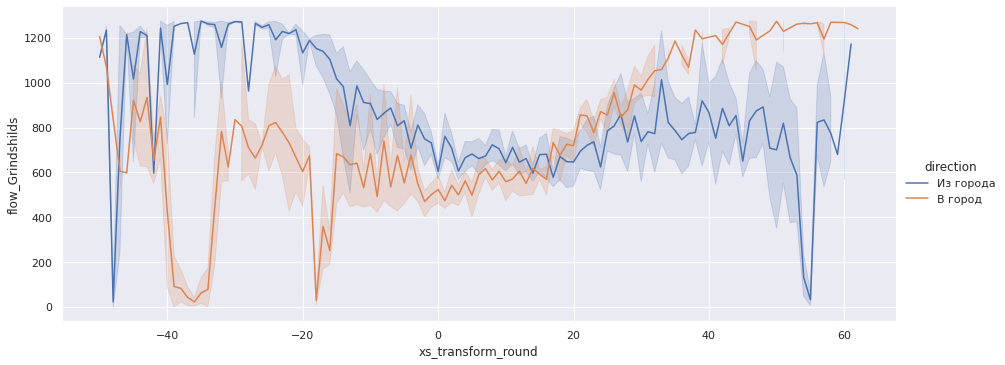
cross = gps_data.query('-10 < xs_transform < 25')
mean_flow_Tanaka = cross.flow_Tanaka.mean()
print(f"Средняя пропускная способность по модели Танака - {mean_flow_Tanaka:.1f} авт/ч \
или {mean_flow_Tanaka / 60:.1f} авт/мин")
Средняя пропускная способность по модели Танака — 1275.5 авт/ч или 21.3 авт/мин
mean_flow_Grindshilds = cross.flow_Grindshilds.mean()
print(f"Средняя пропускная способность по модели Гриндшилдса - {mean_flow_Grindshilds:.1f} авт/ч \
или {mean_flow_Grindshilds / 60:.1f} авт/мин")
Средняя пропускная способность по модели Гриндшилдса — 660.0 авт/ч или 11.0 авт/мин
Как видно, наша оценка по модели Гриндшилдса наиболее близка данным эксперимента в 700 авт./ч.
plt.plot(V1, density_Grindshilds(V1)*V1, label="Модель Гриндшилдса")
plt.xlabel(r'Скорость $V$, км/ч')
plt.ylabel(r'Интенсивность $Q$, авт/ч')
plt.show()

Исходя из этой модели, если мы каким-то образом увеличим скорость на переезде всего до 30 км/ч — пропускная способность увеличится почти в два раза.
Примерно тоже самое мы получим при расчете по формуле, введя коэффициент для хорошей ровности дороги:
$$display$$P_{ж.п.}=1500 \cdot 0.93 \cdot 0.98 \cdot 0.8 \cdot 1 \cdot 1 = 1093.7 авт./ч = 18.3 авт./мин$$display$$
Также проблему железнодорожных переездов с предложениями хорошо осветил автор статьи
4. Итоги
Исходя из нашего анализа можно утверждать, что железнодорожный переезд находится в неудовлетворительном состоянии и скорость потока составляется примерно 10 км/ч, что при полной загрузке дороги вызывает затруднение движения и пробки.
Пропускную способность переезда можно существенно повысить при приведение переезда в удовлетворительное состояние.

Для ответа мы немного углубимся в нормативы и теорию транспортных потоков, проанализируем данные GPS и акселерометра с помощью Python и сравним теоретические расчеты с экспериментальными данными.
Содержание
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
-
You must be registered for see links
-
-
You must be registered for see links
1. Исходные данные
Мы имеет одноколейный железнодорожный переезд с плохим качеством дороги, скорость на котором примерно 10 км/ч. Из подручных средств современный смартфон и ноутбук.
Весь код и данные доступны в формате Jupyter Notebook на моем
You must be registered for see links
.
Нам понадобятся следующие библиотеки:
import pandas as pd
import numpy as np
import glob
#!pip install utm
import utm
from sklearn.decomposition import PCA
from scipy import interpolate
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(rc={'figure.figsize'
import plotly.express as px
# Токен Mapbox для карт в Plotly
mapbox_token = open('mapbox_token', 'r').read()
2. Теория транспортного потока
Для начала определимся с терминами.
Плотность движения $inline$\rho$inline$ — Число автомобилей на 1 км дороги.
$inline$v$inline$ — скорость АТС.
Интенсивность движения $inline$Q(\rho)$inline$ — Количество транспортных средств, проходящие в единицу времени через определенное сечение дороги.
Пропускная способность $inline$P$inline$ — Максимальное число автомобилей, которое может пропустить участок дороги в единицу времени в одном или двух направлениях в рассматриваемых дорожных и погодно-климатических условиях.
Плотность движения и интенсивность связаны формулой:
$$display$$Q = V \cdot \rho$$display$$
Зависимость $inline$Q(\rho)$inline$ часто называют фундаментальной диаграммой.
Так на графике ниже отображены экспериментальные данные «Центра исследования транспортной инфраструктуры» г. Москвы, собранные в течение одного дня в 2005 г. по четырем полосам на участке третьего транспортного кольца от Автозаводской улицы до Варшавского шоссе, и сагрегированные на одну полосу.

Оценка пропускной способности
Основным документом при оценке пропускной способности дорог и их элементов является документ
You must be registered for see links
"Методические рекомендации по оценке пропускной способности автомобильных дорог".Для железнодорожных переездов выделен целый раздел, и пропускная способность в разных дорожных условиях рассчитывается по формуле:
$$display$$P_{ж.п.}=P_д \cdot \beta^{ж.п.}_1 \cdot \beta^{ж.п.}_2 \cdot \beta^{ж.п.}_3 \cdot \beta^{ж.п.}_4 \cdot \beta^{ж.п.}_5,$$display$$
где $inline$\beta^{ж.п.}_1,\beta^{ж.п.}_2,\beta^{ж.п.}_3,\beta^{ж.п.}_4,\beta^{ж.п.}_5$inline$ — коэффициенты снижения пропускной способности, учитывающие состав движения, характеристики железнодорожных переездов и дорожные условия в зоне переезда, которые определяются по приведенным таблицам.
Рассчитаем пропускную способность, исходя из наших условий:
$$display$$P_{ж.п.}=1500 \cdot 0.93 \cdot 0.66 \cdot 0.8 \cdot 1 \cdot 1 = 736.56 авт./ч = 12.3 авт./мин$$display$$
Мы получили теоретическую оценку, теперь перейдем к тому, что есть на самом деле.
В реальных условиях я использовал 2 метода оценки пропускной способности:
- Непосредственный подсчет проехавших через переезд АТС;
- Вычисление средней скорости движения АТС в выделенной нами области и применение различных функционалов для определения плотности.
В качестве функционала можно использовать простые модели:
- Модель Танака:
$inline$\rho(v)=\frac{1}{d(v)}$inline$,
$inline$d(v)= L+ c_1 v+ c_2 v^2$inline$,
где $inline$d(v)$inline$ – среднее (безопасное) расстояние между АТС, $inline$L$inline$ – средняя длина АТС, $inline$c_1$inline$ – время, характеризующее реакцию водителя, $inline$c_2$inline$ — коэффициент пропорциональности тормозному пути. При нормальных условиях (сухой асфальт): $inline$L=5.7 м, c_1=0.504 c, c_2=0.0285 с^2/м$inline$.
- Модель Гриндшилдса:
$inline$\rho= \rho_{max} (1 - \frac{v}{v_{max}})$inline$,
где $inline$\rho_{max}$inline$ — максимальная плотность потока (при отсутствии движения), $inline$v_{max}$inline$ — максимальная (желаемая) скорость движения АТС (при пустой дороге). Эти данные можно взять из того же ОДМ 218.2.020-2012 — $inline$\rho_{max} = 85 авт./км, v_{max}=60 км/ч$inline$
Код для графиков
# Загрузка данных для Диаграммы уравнения потока
diagram1 = pd.read_csv('Диаграмма уравнения потока.csv', sep=';', header=None, names=['P', 'V'], decimal=',')
diagram1_func = interpolate.interp1d(diagram1['P'], diagram1['V'], kind='cubic')
diagram1_xnew = np.arange(diagram1['P'].min(), diagram1['P'].max())
# Загрузка данных для Фундаментальной диаграммы
diagram2 = pd.read_csv('Фундаментальная диаграмма.csv', sep=';', header=None, names=['P', 'Q'], decimal=',')
diagram2_func = interpolate.interp1d(diagram2['P'], diagram2['Q'], kind='cubic')
diagram2_xnew = np.arange(diagram2['P'].min(), diagram2['P'].max())
def density_Tanaka(V):
# Функция плотности для модели Танака
V = V * 1000 / 60 / 60 # переводим км/ч в м/с
L = 5.7 # м
c1 = 0.504 # с
c2 = 0.0285 #с**2/м
return 1000 / (L + c1 * V + c2 * V**2) # авт./км
def density_Grindshilds(V):
# Функция плотности для модели Гриндшилдса
pmax = 85 # авт./км
vmax = 60 # км/ч
return pmax * (1 - V / vmax) # авт./км
# Построение графиков
V = np.arange(1, 80) # км/ч
V1 = np.arange(1, 61) # км/ч
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))
ax1.plot(density_Tanaka(V), V, label="Модель Танака")
ax1.plot(density_Grindshilds(V1), V1, label="Модель Гриндшилдса")
ax1.plot(diagram1_xnew, diagram1_func(diagram1_xnew), label="Экспер. данные ТТК")
ax1.set_xlabel(r'Плотность $\rho$, авт/км')
ax1.set_ylabel(r'Скорость $V$, км/ч')
ax1.legend()
ax2.plot(density_Tanaka(V), density_Tanaka(V) * V, label="Модель Танака")
ax2.plot(density_Grindshilds(V1), density_Grindshilds(V1) * V1, label="Модель Гриндшилдса")
ax2.plot(diagram2_xnew, diagram2_func(diagram2_xnew), label="Экспер. данные ТТК")
ax2.set_xlabel(r'Плотность $\rho$, авт/км')
ax2.set_ylabel(r'Интенсивность $Q$, авт/ч')
ax2.legend()
plt.show()

Модель Гриндшилдса с исходными данными для переезда существенно занижает интенсивность по сравнению с экспериментальными данными для обычной дороги. Давайте сравним эту модель с реальностью.
3. Сбор и анализ данных
3.1 Ручной подсчет интенсивности движения
Я не стал усложнять и применять нейронные сети для распознавания машин, а просто написал кейлогер с сохранением времени и нажатой клавиши. Чтобы после каждого нажатия не вводить Enter, код немного усложнился:
Код кейлогера
%%writefile "key-logger.py"
import pandas as pd
import time
import datetime
class _GetchUnix:
# from
You must be registered for see links
def __init__(self):
import tty, sys
def __call__(self):
import sys, tty, termios
fd = sys.stdin.fileno()
old_settings = termios.tcgetattr(fd)
try:
tty.setraw(sys.stdin.fileno())
ch = sys.stdin.read(1)
finally:
termios.tcsetattr(fd, termios.TCSADRAIN, old_settings)
return ch
def logging():
path = 'logs/keylog/'
filename = f"{time.strftime('%Y-%m-%d %H-%M-%S')}.csv"
path_to_file = path + filename
db = []
getch = _GetchUnix()
print('Процесс...')
while True:
key = getch()
if key == 'c':
break
else:
db.append((datetime.datetime.now(), key))
df = pd.DataFrame(db, columns=['time', 'click'])
print(df)
df.to_csv(path_to_file, index=False)
print(f"\nSaved to {filename}")
if __name__ == "__main__":
logging()
Пришлось посидеть возле переезда 20 минут и внимательно смотреть за потоком. Я записал 2 периода сразу после проезда поезда, т. е. при загрузке переезда на 100%:
files = glob.glob('logs/keylog/*.csv')
keylogger_data = []
print(f'Количество файлов - {len(files)} шт.')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'])
keylogger_data.append(df)
keylogger_data = pd.concat(keylogger_data, ignore_index=True)
keylogger_data.head()
| time | click | � |
|---|---|---|
| 0 | 2020-09-29 16:24:02.691189 | d |
| 1 | 2020-09-29 16:24:05.186670 | a |
| 2 | 2020-09-29 16:24:07.157702 | d |
| 3 | 2020-09-29 16:24:11.506961 | a |
| 4 | 2020-09-29 16:24:14.206266 | a |
Клавиша "a" — машина проехала через переезд из города, клавиша 'd' — в город.
Сагрегируем данные по минутам и направлению:
keylogger_data['time'] = keylogger_data['time'].astype('datetime64[m]')
keylogger_per_min = keylogger_data.groupby(['click', 'time'], as_index=False).size().reset_index().rename(columns={0:'size'})
keylogger_per_min.head()
| index | click | time | size | � |
|---|---|---|---|---|
| 0 | 0 | a | 2020-09-29 16:24:00 | 12 |
| 1 | 1 | a | 2020-09-29 16:25:00 | 13 |
| 2 | 2 | a | 2020-09-29 16:26:00 | 9 |
| 3 | 3 | a | 2020-09-29 16:27:00 | 18 |
| 4 | 4 | a | 2020-09-29 16:28:00 | 14 |
sns.catplot(x='click', y='size', kind="box", data=keylogger_per_min);

print(f"Средняя пропускная способность: {keylogger_per_min['size'].mean():.1f} авт./мин \
или {keylogger_per_min['size'].mean() * 60:.1f} авт./ч")
Средняя пропускная способность: 11.7 авт./мин или 700.0 авт./ч
Экспериментальная интенсивность почти соответствуют расчетной с неудовлетворительным состоянием переезда.
Вспомним нашу модель Гриндшилдса — интенсивности в 700 авт./ч соответствует скорость около 10 км/ч (о 50 км/ч речи не идет) — по ощущения при переезде это так и есть.
plt.plot(V1, density_Grindshilds(V1)*V1, label="Модель Гриндшилдса")
plt.xlabel(r'Скорость $V$, км/ч')
plt.ylabel(r'Интенсивность $Q$, авт/ч')
plt.show()

3.2 Измерение средней скорости на переезде
Для измерения скорости я использовал приложение для Android GPSLogger с сохранением трекинга в csv файлы. В процессе написания статьи возникла идея посмотреть на данные акселерометра (линейного ускорения) с привязкой данных GPS — с этим отлично справилось приложение Physics Toolbox Suite.
За всё время у меня набралось около 50 проходов переезда. Данные записывались и при нулевом трафике и в пробках — я старался проезжать переезд со скоростью потока.
Загрузим все данные, при этом сразу добавим информацию о направлении движения — это понадобится в дальнейшем для графиков.
Данные приложения GPSLogger
Приложение GPSLogger сохраняет много информации, но нам потребуется только:
- time — дата и время;
- lat и lon — широта и долгота, град;
- speed — скорость, $inline$м/с^2$inline$;
- direction — направление, в город или из города.
files = glob.glob('logs/gps/*.csv')
gpslogger_data = []
print(f'Количество файлов с данными GPS - {len(files)} шт.')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'], index_col='time')
if df.iloc[10, 1] < df.iloc[-1, 1]:
df['direction'] = 0 # в город
else:
df['direction'] = 1 # из города
gpslogger_data.append(df)
gpslogger_data = pd.concat(gpslogger_data)
gpslogger_data.head()
gps_1 = gpslogger_data[['lat', 'lon', 'speed', 'direction']]
Количество файлов с данными GPS — 37 шт.
Данные приложения Physics Toolbox Suite:
files = glob.glob('logs/gps_accel/*.csv')
print(f'Количество файлов с данными акселерометра - {len(files)} шт.')
pts_data = []
for filename in files:
df = pd.read_csv(filename, sep=';',decimal=',')
df['time'] = filename[-22:-12] + '-' + df['time']
if df.iloc[10, 5] < df.iloc[-1, 5]:
df['direction'] = 0 # в город
else:
df['direction'] = 1 # из города
pts_data.append(df)
pts_data = pd.concat(pts_data)
pts_data.head()
Количество файлов с данными акселерометра — 14 шт.
| time | ax | ay | az | Latitude | Longitude | Speed (m/s) | Unnamed: 7 | direction | � |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2020-09-04-14:11:18:029 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.00000 | 0.0 | NaN | 1 |
| 1 | 2020-09-04-14:11:18:030 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 2 | 2020-09-04-14:11:18:030 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 3 | 2020-09-04-14:11:18:094 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 4 | 2020-09-04-14:11:18:094 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
Данные содержат некорректные записи с нулевой широтой, долготой — почистим:
pts_data = pts_data.query('Latitude != 0.')
Приложение Physics Toolbox Suite записывает данные с максимальной частотой для акселерометра 400 Гц, но датчик GPS работает с частотой 1 Гц, поэтому разделим данные по датчикам:
pts_data['time'] = pd.to_datetime(pts_data['time'], format='%Y-%m-%d-%H:%M:%S:%f')
pts_data = pts_data.rename(columns={'Latitude':'lat', 'Longitude':'lon', 'Speed (m/s)':'speed'})
Данные акселерометра:
accel_data = pts_data[['time', 'lat', 'lon', 'ax', 'ay', 'az', 'direction']].copy()
accel_data = accel_data.set_index('time')
accel_data['direction'] = accel_data['direction'].map({1.: 'Из города', 0.: 'В город'})
accel_data.head()
| lat | lon | ax | ay | az | direction | � |
|---|---|---|---|---|---|---|
| time | � | |||||
| 2020-09-04 14:11:18.030 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | Из города |
| 2020-09-04 14:11:18.030 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | Из города |
| 2020-09-04 14:11:18.094 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | Из города |
| 2020-09-04 14:11:18.094 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | Из города |
| 2020-09-04 14:11:18.095 | 56.372343 | 37.53044 | 0.0 | 0.0 | -0.0 | Из города |
Данные GPS:
gps_2 = pts_data[['time', 'lat', 'lon', 'speed', 'direction']].copy()
gps_2 = gps_2.set_index('time')
gps_2 = gps_2.resample('S').mean()
gps_2 = gps_2.dropna(how='all')
gps_2.head()
| lat | lon | speed | direction | � |
|---|---|---|---|---|
| time | � | |||
| 2020-08-10 00:45:02 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:03 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:04 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:05 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:06 | 56.338342 | 37.522946 | 0.0 | 1.0 |
Объединим все GPS данные:
gps_data = gps_1.append(gps_2, ignore_index=True)
gps_data['direction'] = gps_data['direction'].map({1.: 'Из города', 0.: 'В город'})
gps_data.head()
| lat | lon | speed | direction | � |
|---|---|---|---|---|
| 0 | 56.167241 | 37.504026 | 19.82 | Из города |
| 1 | 56.167051 | 37.503804 | 19.36 | Из города |
| 2 | 56.166884 | 37.503667 | 19.62 | Из города |
| 3 | 56.166718 | 37.503554 | 19.35 | Из города |
| 4 | 56.166570 | 37.503427 | 19.12 | Из города |
3.2.1 Визуализация на карте
Визуализируем данные на карте с помощью библиотеки Plotly:
fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()

3.2.2 Визуализация профиля переезда
Чтобы построить график продольного сечения переезда нужно выполнить два преобразования:
- Перевести координаты GPS, а это обычно система координат WGS 84 в плоскую проекцию.
- Спроецировать данные на профиль дороги.
В сервисах онлайн карт обычно используется проекция Web Mercator, которая имеет один недостаток — это сильное искажение расстояний, именно поэтому Гренландия на картах выглядит больше Африки, хотя на самом деле меньше в несколько раз.
Для геодезических и картографических работ применяются проекции, основанные на поперечной проекции Меркатора. В России и многих других странах применяется проекция Гаусса — Крюгера, в США — универсальная поперечная проекция Меркатора (UTM).
Проекция Web-Mercator

Проекция UTM

Для преобразования в UTM для Python есть простое решение
You must be registered for see links
, его и будем использовать.gps_data['xs'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
gps_data['ys'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
gps_data['speed_kmh'] = gps_data.speed / 1000 * 60 * 60
Оставим данные только вокруг переезда в радиусе 50 метров:
# Координаты переезда
lat0 = 56.35205
lon0 = 37.51792
xc, yc, _, _ = utm.from_latlon(lat0, lon0)
r = 50
gps_data = gps_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')
fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()

Теперь спроецируем точки на ось дороги. Это по сути задача понижения размерности с 2d в 1d, которая решается методом главных компонент (PCA).
Мы можем поступить 2 способами — вручную вычислить матрицу поворота и взять одну компоненту или довериться реализации scikit-learn. Для простоты выберем Sklearn:
pca = PCA(n_components=1).fit(gps_data[['xs', 'ys']])
gps_data['xs_transform'] = pca.transform(gps_data[['xs', 'ys']])
sns.relplot(x='xs_transform', y='speed_kmh', data=gps_data, aspect=2.5, hue='direction');

В большинстве случаев после переезда скорость возрастает. По графику можно выделить границы переезда — это примерно интервал [-5, 25]. Для уточнения посмотрим на данные с акселерометра.
accel_data['xs'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
accel_data['ys'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
accel_data = accel_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')
accel_data['xs_transform'] = pca.transform(accel_data[['xs', 'ys']])
Оси акселерометра в Android располагаются следующим образом:

При записи данных телефон всегда лежал по ходу движения (ось Y). Посмотрим на графики отдельно по осям:
sns.relplot(x='xs_transform', y='ax', data=accel_data, aspect=2.5, hue='direction');

sns.relplot(x='xs_transform', y='ay', data=accel_data, aspect=2.5, hue='direction');

sns.relplot(x='xs_transform', y='az', data=accel_data, aspect=2.5, hue='direction');

Увеличим масштаб по оси Z:
sns.relplot(x='xs_transform', y='az', data=accel_data.query('-20 < xs_transform < 40'), aspect=2.5, hue='direction');

По осям X и Z четко определяются границы переезда — интервал [-10, 25] с центром в точке 7.5.
cross = gps_data.query('-10 < xs_transform < 25')
fig = px.scatter_mapbox(cross, lat="lat", lon="lon", color='direction', zoom=19, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()

Теперь посмотрим как распределена скорость на переезде:
mean_v = cross.speed_kmh.mean()
print(f"Средняя скорость на переезде - {mean_v:.2} км/ч")
sns.distplot(cross.speed_kmh);
Средняя скорость на переезде — 9.4 км/ч

Округлим координаты до метра и построим еще немного красивых графиков:
base = 1
gps_data['xs_transform_round'] = gps_data['xs_transform'].apply(lambda x: base * round(x / base))
accel_data['xs_transform_round'] = accel_data['xs_transform'].apply(lambda x: base * round(x / base))
sns.relplot(x='xs_transform_round', y='speed_kmh', data=gps_data, kind="line", aspect=2.5);

sns.relplot(x='xs_transform_round', y='az', data=accel_data, kind="line", aspect=2.5);

3.3 Оценка плотности
Для расчета пропускной способности используем две модели для плотности:
gps_data['flow_Tanaka'] = density_Tanaka(gps_data.speed_kmh) * gps_data.speed_kmh
gps_data['flow_Grindshilds'] = density_Grindshilds(gps_data.speed_kmh) * gps_data.speed_kmh
sns.relplot(x='xs_transform_round', y='flow_Grindshilds', data=gps_data, aspect=2.5, kind='line', hue='direction');

cross = gps_data.query('-10 < xs_transform < 25')
mean_flow_Tanaka = cross.flow_Tanaka.mean()
print(f"Средняя пропускная способность по модели Танака - {mean_flow_Tanaka:.1f} авт/ч \
или {mean_flow_Tanaka / 60:.1f} авт/мин")
Средняя пропускная способность по модели Танака — 1275.5 авт/ч или 21.3 авт/мин
mean_flow_Grindshilds = cross.flow_Grindshilds.mean()
print(f"Средняя пропускная способность по модели Гриндшилдса - {mean_flow_Grindshilds:.1f} авт/ч \
или {mean_flow_Grindshilds / 60:.1f} авт/мин")
Средняя пропускная способность по модели Гриндшилдса — 660.0 авт/ч или 11.0 авт/мин
Как видно, наша оценка по модели Гриндшилдса наиболее близка данным эксперимента в 700 авт./ч.
plt.plot(V1, density_Grindshilds(V1)*V1, label="Модель Гриндшилдса")
plt.xlabel(r'Скорость $V$, км/ч')
plt.ylabel(r'Интенсивность $Q$, авт/ч')
plt.show()

Исходя из этой модели, если мы каким-то образом увеличим скорость на переезде всего до 30 км/ч — пропускная способность увеличится почти в два раза.
Примерно тоже самое мы получим при расчете по формуле, введя коэффициент для хорошей ровности дороги:
$$display$$P_{ж.п.}=1500 \cdot 0.93 \cdot 0.98 \cdot 0.8 \cdot 1 \cdot 1 = 1093.7 авт./ч = 18.3 авт./мин$$display$$
Также проблему железнодорожных переездов с предложениями хорошо осветил автор статьи
You must be registered for see links
.4. Итоги
Исходя из нашего анализа можно утверждать, что железнодорожный переезд находится в неудовлетворительном состоянии и скорость потока составляется примерно 10 км/ч, что при полной загрузке дороги вызывает затруднение движения и пробки.
Пропускную способность переезда можно существенно повысить при приведение переезда в удовлетворительное состояние.


