- Регистрация
- 23.09.18
- Сообщения
- 12.347
- Реакции
- 176
- Репутация
- 0
Пока в мире распознавания объектов обучают десятки и даже сотни зарекомендовавших себя архитектур искусственных нейронных сетей (ИНС), разогревая планету мощными видеокарточками и создавая «панацею» для всех задач компьютерного зрения, мы в Smart Engines твердо идем по исследовательскому пути, предлагая новые эффективные архитектуры ИНС для решения конкретных задач. Сегодня мы расскажем про ХафНет – новый способ поиска точек схода на изображениях.
Преобразование Хафа и его быстрая реализация
По мере развития технологий зрительных систем непрерывно пополнялся список необходимых для этого базовых алгоритмических инструментов. Так, стандартным для любого фреймворка обработки изображений и распознавания образов уже считается наличие морфологической фильтрации, эффективного вычисления свёрток, выделения границ, цветовой адаптации. Все чаще в список базовых инструментов попадает преобразование Хафа (дискретное преобразование Радона). Преобразование Хафа (ПХ) используется для детекции прямолинейных объектов или их различных конфигураций на изображении: детекции дорожной разметки, поиска границ документа, цветовой сегментации, вычислительной томографии и т.д. Алгоритм показывает очень высокие показатели в части детекции и существенно устойчивее к одновременно присутствующим аддитивному координатному и выбросовому шумам, чем, например, метод наименьших квадратов, про это, кстати уже писали на
You must be registered for see links
.Рассмотрим произвольную точку (x[SUB]i[/SUB],y[SUB]i[/SUB]). Через данную точку проходит бесконечное множество прямых, удовлетворяющих уравнению y[SUB]i[/SUB]=x[SUB]i[/SUB]a+b при различных параметрах a и b. Если переписать это уравнение в виде b=-x[SUB]i[/SUB]a+y[SUB]i[/SUB] и рассмотреть плоскость ab, называемую пространством параметров, то для заданной точки (x[SUB]i[/SUB],y[SUB]i[/SUB]) на исходном изображении получаем уравнение единственной прямой в пространстве параметров. Самое важное свойство заключается в следующем: если три точки лежат на одной прямой на изображении, то соответствующие три линии в пространстве параметров пересекаются в одной точке, причем координаты данной точки однозначно определяют параметры той самой прямой, на которой лежали точки на исходном изображении. В представленной параметризации есть недостаток: если искомая прямая близка к вертикали, то ее угловой коэффициент стремится к бесконечности. Поэтому на практике используются другие варианты параметризации прямых (если интересно – пишите в комментариях, мы подготовим про это отдельную статью).
Таким образом, результатом преобразования Хафа от изображения является другое изображение, размер которого определяется допустимыми значениями параметров прямых, а значение пикселя – это сумма интенсивностей пикселей на соответствующей прямой на исходном изображении.
Если на исходном изображении были линии, то на преобразовании Хафа будут ярко выраженные локальные максимумы. Координаты данных максимумов как раз и определяют параметры соответствующих линий на исходном изображении Следующий рисунок показывает результаты преобразования Хафа для изображения с двумя пересекающимися прямыми.

Несмотря на такую высокую практическую ценность, у преобразования Хафа есть один критический недостаток, который часто тормозит применение преобразование Хафа на практике: классическая реализация преобразования Хафа обладает высокой вычислительной сложностью – O(n[SUP]3[/SUP]), где n – линейный размер исследуемого изображения.
Зато на практике часто используют так называемое быстрое преобразование Хафа (БПХ) – алгоритм, вычисляющий приближенное значение преобразования Хафа, использующий диадический паттерн (ДП) для аппроксимации прямых на изображении. Сложность БПХ оценивается как O(n[SUP]2[/SUP] log(n)), что существенно приятнее с вычислительной точки зрения. Хоть сколько угодно подробное описание алгоритма БПХ выходит за рамки данной статьи, оно может быть найдено, например, в научной работе [5]. Здесь отметим лишь важную особенность алгоритма БПХ, которая будет нам необходима далее при изложении предлагаемой архитектуры нейронной сети: алгоритм БПХ задает четыре квадранта прямых: «преимущественно вертикальные с отрицательным сдвигом» (будем обозначать H[SUB]1[/SUB]), «преимущественно вертикальные с положительным сдвигом» (будем обозначать H[SUB]2[/SUB]), «преимущественно горизонтальные с отрицательным сдвигом» (будем обозначать H[SUB]3[/SUB]) и «преимущественно горизонтальные с положительным сдвигом» (будем обозначать H[SUB]4[/SUB]). Кроме того, будем обозначать H[SUB]12[/SUB] и H[SUB]34[/SUB] преимущественно вертикальные и преимущественно горизонтальные соответственно, полученные путем объединения соответствующих квадрантов.
Детекция точки схода с помощью БПХ
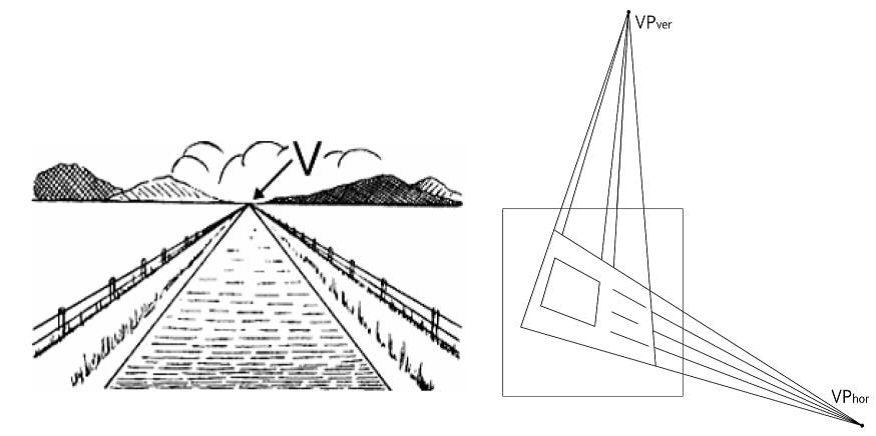
Теперь мы готовы разобраться с принципом детекции точек схода на изображении с помощью преобразования Хафа (а точнее, с помощью алгоритма быстрого преобразования Хафа). Напомним, что точкой схода называется точка, в которой сходятся на перспективном изображении параллельные линии рассматриваемой сцены. Множество соответствующих линий называется пучком.
В зависимости от специфики сцены может быть разное количество точек схода. Так, например, когда мы фотографируем какой-нибудь документ, то обычно на изображении присутствует две точки схода: первая за счет наличия горизонтальных линий (как реальных, так и воображаемых, как например верхняя и нижняя границы документа), а вторая – за счет вертикальных линий. Последовательное двухкратное применение БПХ позволяет найти эти точки схода, что далее может быть использовано для исправления перспективы. Поясним это на примере. Рассмотрим пучек из четырех линий, которые пересекаются где-то далеко за пределами изображения. Если к данному изображению применить БПХ, то на изображении H[SUB]12[/SUB] увидим четыре локальных максимума, каждый из которых соответствует прямой на исходном изображении. Теперь, если повторно применить БПХ, то изображение H[SUB]34[/SUB] будет содержать только один локальный максимум, по координатам которого можно однозначно определить координаты исходной точки схода. Кстати, интересной деталью является то, что сумма по всем строкам на картинке H[SUB]12[/SUB] одинакова, и, следовательно, считать преобразование Хафа по горизонтальным линиям не имеет смысла. Поэтому необходимо погасить шум (в данном случае, мы возвели интенсивность изображения H[SUB]12[/SUB] в квадрат).

Аналогичные рассуждения применяются для поиска второй точки схода (образованной горизонтальными линиями документа). Имея обе точки схода, можно уже исправлять перспективу изображения и получать на выходе ровненький документ (ибо ровный документ – залог качественного распознавания).
У любопытного читателя Хабра, который дочитал статью до этого абзаца, наверняка уже зреет только одна мысль: так где же нейронные сети? Кажется, описанный выше алгоритм крайне понятен и не требует никакого машинного обучения… Так вот, в следующем разделе мы готовы дать ответ на этот ключевой вопрос!
Искусственная нейронная сеть поиска точек схода HoughNet
Вся соль описанного выше алгоритма поиска точек схода заключается в том, что успешно применять его можно только на изображениях, где соответствующие линии как-то одинаково сегментированы (например, как показано выше – линии задаются белыми пикселями, а все остальное – черными). Но такая «идеальная» картина мира встречается крайне редко (а по правде говоря, не встречается вообще никогда). Поэтому перед вызовом преобразования Хафа всегда применяется «правильная» фильтрация. Только как подобрать эту «правильную» фильтрацию, если про сцену, которая зафиксирована на изображении не известно практически ничего?
Подумав, мы разработали архитектуру нейронной сети (мы назвали ее HoughNet), в которой присутствует два слоя, вычисляющих Хаф-образ и три группы сверточных слоев. В такой комбинации сверточные слои решают задачи предварительной фильтрации, локализации локальных максимумов и вычисления дополнительных статистик, а преобразование Хафа – преобразование координат, которое позволяет нейронной сети работать не с локальными интенсивностями пикселей, а с интегральными статистиками вдоль прямолинейных объектов. Кстати, способ обучения такой нейронной сети тоже нетривиален (за важными подробностями обращайтесь в [1]).
| Номер слоя | Тип слоя | Параметры | Функция активации |
|---|---|---|---|
1 | conv | 12 filters 5x5, stride 1x1, no padding | relu |
2 | conv | 12 filters 5x5, stride 2x2, no padding | relu |
3 | conv | 12 filters 5x5, stride 1x1, no padding | relu |
4 | FHT | H12 for vertical, H34 for horizontal | - |
5 | conv | 12 filters 3x9, stride 1x1, no padding | relu |
6 | conv | 12 filters 3x5, stride 1x1, no padding | relu |
7 | conv | 12 filters 3x9, stride 1x1, no padding | relu |
8 | conv | 12 filters 3x5, stride 1x1, no padding | relu |
9 | FHT | H34 for both branchesg | - |
10 | conv | 16 filters 5x5, stride 3x3, no padding | relu |
11 | conv | 16 filters 5x5, stride 3x3, no padding | relu |
12 | conv | 1 filter 5x5, stride 3x3, no padding | 1 – rbf |
Представленная нейронная сеть порождает два изображения: одно для поиска «вертикальной» точки схода, а второе для поиска «горизонтальной» точки схода. На каждом изображении точка с максимальным значением яркости является соответствующим ответом.
Перейдем к экспериментам. Мы обучили нашу сеточку на
You must be registered for see links
[6]. Этот датасет содержит изображения различных документов, сфотографированных на мобильные устройства. Всего в датасете представлено 50 типов документов. Чуть больше половины датасета (а именно, первые 30 типов документов) использовалось для обучения, оставшаяся часть – для оценки качества работы обученной сети.Несмотря на то, что мы обучались на фотографиях документов, мы применили обученную сеть в качестве предварительного этапа распознавания на датасете ICDAR 2011 dewarping contest dataset (который содержит 100 черно-белых изображений документов, полученных различным методом и содержащих различные геометрические искажения) и замерили качество полнотекстового распознавания.

Получилось превзойти по качеству не только «сырое» распознавание (распознавание неисправленного изображения), но и текущий state-of-the-art [7] и [8].
| Исходное изображение | Алгоритм [7] | Алгоритм [8] | HoughNet | � |
|---|---|---|---|---|
Качество распознавания | 31.3% | 49.6% | 50.1% | 59.7% |
Список использованной литературы
При написании настоящей статьи использовались материалы из следующих источников
[1] Sheshkus A. et al. HoughNet: neural network architecture for vanishing points detection // 2019 International Conference on Document Analysis and Recognition (ICDAR). – 2020. doi: 10.1109/ICDAR.2019.00140.
[2] Алиев М. А., Николаев Д. П., Сараев А. А. Построение быстрых вычислительных схем настройки алгоритма бинаризации Ниблэка // Труды Института системного анализа Российской академии наук. – 2014. – Т. 64. – №. 3. – С. 25-34.
[3] Ершов Е.И. Быстрое преобразование Хафа как инструмент анализа двумерных и трехмерных изображений в задачах поиска прямых и линейной кластеризации: Автореф. … дис. канд. физ.-мат. наук. – М., 2019. – 24 с.
[4] Преобразование Хафа [Электронный ресурс]: Википедия. Свободная энциклопедия. – Режим доступа:
You must be registered for see links
(дата обращения: 13.03.2020).[5] Nikolaev D. P., Karpenko S. M., Nikolaev I. P., Nikolayev P. P. Hough Transform: Underestimated Tool in the Computer Vision Field // 22st European Conference on Modelling and Simulation, ECMS 2008. – Nicosia, Cyprys, 2008. – P. 238–243.
[6] Arlazarov V. V. et al. MIDV-500: a dataset for identity document analysis and recognition on mobile devices in video stream // Компьютерная оптика. – 2019. – Т. 43. – №. 5.
[7] Y. Takezawa, M. Hasegawa, and S. Tabbone, “Cameracaptured document image perspective distortion correction using vanishing point detection based on radon transform,” in Pattern Recognition (ICPR), 2016 23rd International Conference on. IEEE, 2016, pp. 3968–3974.
[8] Y. Takezawa, M. Hasegawa, and S. Tabbone, “Robust perspective rectification of camera-captured document images,” in Document Analysis and Recognition (ICDAR), 2017 14th IAPR International Conference on, vol. 6. IEEE, 2017, pp. 27–32.

