- Регистрация
- 14.05.16
- Сообщения
- 11.398
- Реакции
- 501
- Репутация
- 0
Детектирование аномалий — интересная задача машинного обучения. Не существует какого-то определенного способа ее решения, так как каждый набор данных имеет свои особенности. Но в то же время есть несколько подходов, которые помогают добиться успеха. Я хочу рассказать про один из таких подходов — автоенкодеры.
Какой датасет выбрать?
Самый актуальный вопрос в жизни любого дата-саентиста. Чтобы упростить повествование, я буду использовать простой по структуре датасет, который сгенерируем здесь же.
# импортируем библиотеки
import os
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
# функция для генерации нормального распределения с заданными параметрами
def gen_normal_distribution(mu, sigma, size, range=(0, 1), max_val=1):
bins = np.linspace(*range, size)
result = 1 / (sigma * np.sqrt(2*np.pi)) * np.exp(-(bins - mu)**2 / (2*sigma**2))
cur_max_val = result.max()
k = max_val / cur_max_val
result *= k
return result
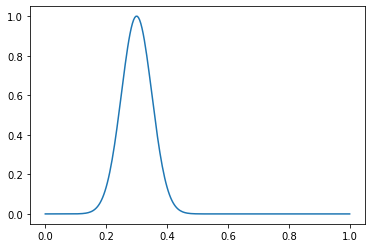
Рассмотрим пример работы функции. Создадим нормальное распределение с μ = 0.3 и σ = 0.05:
dist = gen_normal_distribution(0.3, 0.05, 256, max_val=1)
print(dist.max())
>>> 1.0
plt.plot(np.linspace(0, 1, 256), dist)
Объявим параметры нашего датасета:
in_distribution_size = 2000
out_distribution_size = 200
val_size = 100
sample_size = 256
random_generator = np.random.RandomState(seed=42) # для воспроизводимости используется seed
И функции для генерирования примеров — нормальных и аномальных. Нормальными будут считаться распределения с одним максимумом, аномальными — с двумя:
def generate_in_samples(size, sample_size):
global random_generator
in_samples = np.zeros((size, sample_size))
in_mus = random_generator.uniform(0.1, 0.9, size)
in_sigmas = random_generator.uniform(0.05, 0.5, size)
for i in range(size):
in_samples = gen_normal_distribution(in_mus, in_sigmas, sample_size, max_val=1)
return in_samples
def generate_out_samples(size, sample_size):
global random_generator
# создаем распределение с одним пиком
out_samples = generate_in_samples(size, sample_size)
# и накладываем поверх него еще один небольшой максимум
out_additional_mus = random_generator.uniform(0.1, 0.9, size)
out_additional_sigmas = random_generator.uniform(0.01, 0.05, size)
for i in range(size):
anomaly = gen_normal_distribution(out_additional_mus, out_additional_sigmas, sample_size, max_val=0.12)
out_samples += anomaly
return out_samples
Так выглядит нормальный пример:
in_samples = generate_in_samples(in_distribution_size, sample_size)
plt.plot(np.linspace(0, 1, sample_size), in_samples[42])

А аномальный — так:
out_samples = generate_out_samples(out_distribution_size, sample_size)
plt.plot(np.linspace(0, 1, sample_size), out_samples[42])
Создадим массивы с признаками и метками:
x = np.concatenate((in_samples, out_samples))
# нормальные примеры имеют метку 0, аномальные -- 1
y = np.concatenate((np.zeros(in_distribution_size), np.ones(out_distribution_size)))
# разделение на обучающую/тренировочную выборки
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, shuffle=True, random_state=42)
И позволю себе немного схитрить. Для алгоритмов, работающих в две стадии, потребуется 2 обучающих выборки и 1 тестовая (валидационная). При работе с реальными данными пришлось бы урезать имеющиеся тренировочную и тестовую выборки, но мы можешь догенерировать данные (в больших количествах), чтобы более объективно оценить качество модели:
# создаем валидационную выборку из 100 нормальных и 100 аномальных примеров
x_val_out = generate_out_samples(val_size, sample_size)
x_val_in = generate_in_samples(val_size, sample_size)
x_val = np.concatenate((x_val_out, x_val_in))
y_val = np.concatenate((np.ones(val_size), np.zeros(val_size)))
Модели
Перед тем, как перейти к теме статьи, проверим несколько алгоритмов детектирования аномалий из Sklearn: одноклассовый SVM и изолирующий лес. Это алгоритмы обучения без учителя, то есть они ориентируются только на представление данных, но не на обучающие метки.
# функции для оценки качества моделей
from sklearn.metrics import classification_report
from sklearn.metrics import f1_score
One class SVM
from sklearn.svm import OneClassSVM
OneClassSVM позволяет задать параметр nu — долю аномальных объектов в выборке.
out_dist_part = out_distribution_size / (out_distribution_size + in_distribution_size)
svm = OneClassSVM(nu=out_dist_part)
svm.fit(x_train, y_train)
>>> OneClassSVM(cache_size=200, coef0=0.0, degree=3, gamma='scale', kernel='rbf',
max_iter=-1, nu=0.09090909090909091, shrinking=True, tol=0.001,
verbose=False)
Делаем предсказания на тестовом наборе:
svm_prediction = svm.predict(x_val)
svm_prediction[svm_prediction == 1] = 0
svm_prediction[svm_prediction == -1] = 1
В sklearn есть очень удобная функция — classification_report, она позволяет оценить такие важные для Anomaly detection метрики, как precision и recall, причем для каждого класса:
print(classification_report(y_val, svm_prediction))
>>> precision recall f1-score support
0.0 0.57 0.93 0.70 100
1.0 0.81 0.29 0.43 100
accuracy 0.61 200
macro avg 0.69 0.61 0.57 200
weighted avg 0.69 0.61 0.57 200
Ну, такое. Довольно низкий f1-score свидетельствует о том, что модель плохо справляется с задачей.
Isolation forest
Окей, может быть, брат-близнец случайного леса сможет лучше справиться с задачей?
from sklearn.ensemble import IsolationForest
У изолирующего леса тоже есть параметр, отвечающий за долю аномальных объектов в выборке. Зададим его:
out_dist_part = out_distribution_size / (out_distribution_size + in_distribution_size)
iso_forest = IsolationForest(n_estimators=100, contamination=out_dist_part, max_features=100, n_jobs=-1)
iso_forest.fit(x_train)
>>> IsolationForest(behaviour='deprecated', bootstrap=False,
contamination=0.09090909090909091, max_features=100,
max_samples='auto', n_estimators=100, n_jobs=-1,
random_state=None, verbose=0, warm_start=False)
Classification report? — Classification report!
iso_forest_prediction = iso_forest.predict(x_val)
iso_forest_prediction[iso_forest_prediction == 1] = 0
iso_forest_prediction[iso_forest_prediction == -1] = 1
print(classification_report(y_val, iso_forest_prediction))
>>> precision recall f1-score support
0.0 0.50 0.91 0.65 100
1.0 0.53 0.10 0.17 100
accuracy 0.51 200
macro avg 0.51 0.51 0.41 200
weighted avg 0.51 0.51 0.41 200
RandomForestClassifier
Конечно, всегда стоит проверять какой-нибудь простой вариант типа "а вдруг задача классификации окажется посильной для случайного леса?" Что ж, попробуем:
from sklearn.ensemble import RandomForestClassifier
random_forest = RandomForestClassifier(n_estimators=100, max_features=100, n_jobs=-1)
random_forest.fit(x_train, y_train)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features=100,
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=-1, oob_score=False, random_state=None, verbose=0,
warm_start=False)
random_forest_prediction = random_forest.predict(x_val)
print(classification_report(y_val, random_forest_prediction))
>>> precision recall f1-score support
0.0 0.57 0.99 0.72 100
1.0 0.96 0.25 0.40 100
accuracy 0.62 200
macro avg 0.77 0.62 0.56 200
weighted avg 0.77 0.62 0.56 200
Autoencoder
В общем, случилась довольно обыденная для детектирования аномалий штука: ничего не сработало. Переходим к автокодировщикам.
Принцип работы автоенкодера состоит в том, что модель пытается сначала "сжать" данные, а потом восстановить их. Она состоит из 2 частей: Encoder'а и Decoder'а, которые занимаются сжатием и расшифровкой соответственно.
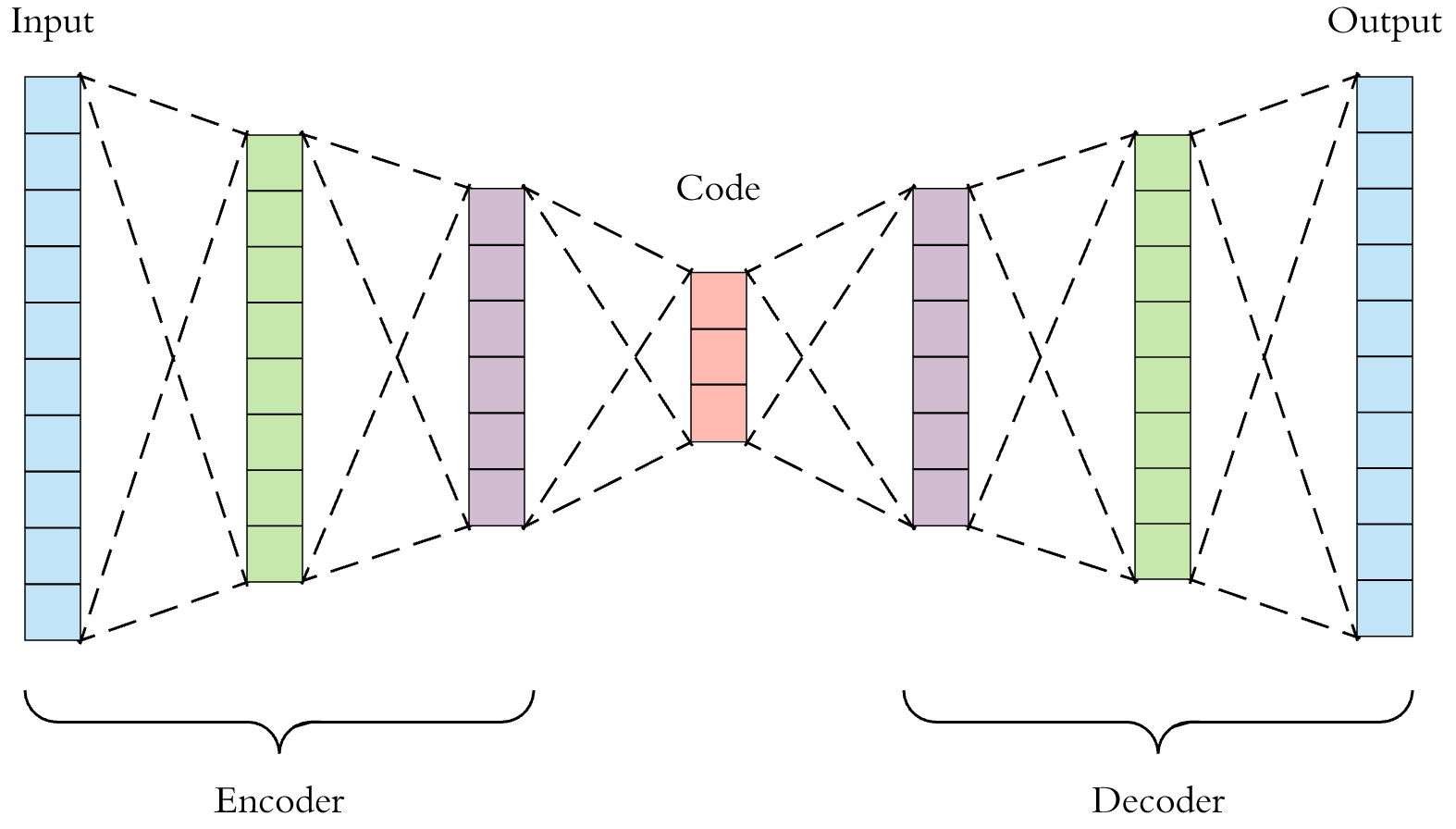
Изображение взято из
Чтобы создать эффект "сжатия" данных, надо уменьшить скрытые слои, заставив их обрабатывать большее количество информации меньшим количеством нейронов.
Как этот эффект поможет нам? Теория информации говорит о том, что чем более вероятно событие, тем меньшее количество информации потребуется, чтобы описать это событие. Вспомним, что у нас всего лишь 9% аномалий и 91% нормальных объектов. Тогда для хранения информации об обычных объектах потребуется меньше информации, чем для запоминания аномальных. Но тогда, если мы подберем правильные параметры нейронной сети, то она сможет запоминать и восстанавливать только обычные объекты: на аномальные ей просто не будет хватать обобщающей способности.
Поэтому восстановленные моделью данные будут значительно отличаться от исходных.
Модель напишем на PyTorch, поэтому импортируем нужные модули:
import torch
from torch import nn
from torch.utils.data import TensorDataset, DataLoader
from torch.optim import Adam
Задаем гиперпараметры модели:
batch_size = 32
lr = 1e-3
Очень важная часть. Тренировочный датасет должен состоять только из обычных объектов, потому что если модель увидит аномальные, то она может "подстроиться" под их восстановление и мы не сможем найти значительные отличия в исходных и восстановленных данных. Конечно, когда гиперпараметры модели (количество нейронов в скрытых слоях, learning rate, размер батча) подобраны правильно, то шанс неудачи понижается, но лучше перестраховаться.
# берем только те примеры из x_train, которые не являются аномальными
train_in_distribution = x_train[y_train == 0]
train_in_distribution = torch.tensor(train_in_distribution.astype(np.float32))
train_in_dataset = TensorDataset(train_in_distribution)
train_in_loader = DataLoader(train_in_dataset, batch_size=batch_size, shuffle=True)
# для теста и валидации возьмем все примеры, чтобы можно было сравнивать работу модели на обычных и аномальных данных
test_dataset = TensorDataset(
torch.tensor(x_test.astype(np.float32)),
torch.tensor(y_test.astype(np.long))
)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
val_dataset = TensorDataset(torch.tensor(x_val.astype(np.float32)))
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
Моделька. Скрытый слой будет иметь размер 4 нейрона, чтобы сымитировать неоптимальные параметры модели (для обычных примеров нам достаточно 2 нейронов: один для задания μ, другой — для σ, так мы полностью опишем распределение; но вот 4 нейрона могут восстановить распределение с двумя максимумами, как в наших аномальных примерах).
class Autoencoder(nn.Module):
def __init__(self, input_size):
super(Autoencoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(input_size, 128),
nn.LeakyReLU(0.2),
nn.Linear(128, 64),
nn.LeakyReLU(0.2),
nn.Linear(64, 16),
nn.LeakyReLU(0.2),
nn.Linear(16, 4),
nn.LeakyReLU(0.2),
)
self.decoder = nn.Sequential(
nn.Linear(4, 16),
nn.LeakyReLU(0.2),
nn.Linear(16, 64),
nn.LeakyReLU(0.2),
nn.Linear(64, 128),
nn.LeakyReLU(0.2),
nn.Linear(128, 256),
nn.LeakyReLU(0.2),
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
model = Autoencoder(sample_size).cuda()
criterion = nn.MSELoss()
per_sample_criterion = nn.MSELoss(reduction="none") # loss для каждого примера, пропущенного через модель
# без параметра reduction="none" pytorch усредняет loss'ы по всем объектам
optimizer = Adam(model.parameters(), lr=lr, weight_decay=1e-5)
Чтобы как-то сравнивать loss'ы на нормальных и аномальных примерах, зададим функцию, строящую boxplot'ы ошибок:
def save_score_distribution(model, data_loader, criterion, save_to, figsize=(8, 6)):
losses = [] # здесь будем хранить loss для каждого объекта выборки
labels = [] # здесь -- метки класса
for (x_batch, y_batch) in data_loader:
x_batch = x_batch.cuda()
output = model(x_batch)
loss = criterion(output, x_batch)
loss = torch.mean(loss, dim=1) # усредняем loss по параметрам модели (то есть оставляем усредненную ошибку для каждого объекта выборки)
loss = loss.detach().cpu().numpy().flatten()
losses.append(loss)
labels.append(y_batch.detach().cpu().numpy().flatten())
losses = np.concatenate(losses)
labels = np.concatenate(labels)
losses_0 = losses[labels == 0] # нормальный класс
losses_1 = losses[labels == 1] # аномальный класс
fig, ax = plt.subplots(1, figsize=figsize)
ax.boxplot([losses_0, losses_1])
ax.set_xticklabels(['normal', 'anomaly'])
plt.savefig(save_to)
plt.close(fig)
На необученной модели функция выдает следующий результат:
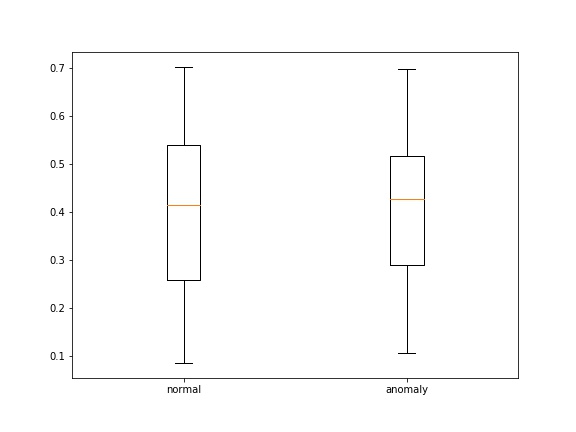
Обучение:
experiment_path = "ood_detection" # папка для сохранения картинок
!rm -rf $experiment_path
os.makedirs(experiment_path, exist_ok=True)
epochs = 100
for epoch in range(epochs):
running_loss = 0
for (x_batch, ) in train_in_loader:
x_batch = x_batch.cuda()
output = model(x_batch)
loss = criterion(output, x_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
print("epoch [{}/{}], train loss:{:.4f}".format(epoch+1, epochs, running_loss))
# сохранение распределений ошибок
plot_path = os.path.join(experiment_path, "{}.jpg".format(epoch+1))
save_score_distribution(model, test_loader, per_sample_criterion, plot_path)
>>>
epoch [1/100], train loss:8.5728
epoch [2/100], train loss:4.2405
epoch [3/100], train loss:4.0852
epoch [4/100], train loss:1.7578
epoch [5/100], train loss:0.8543
...
epoch [96/100], train loss:0.0147
epoch [97/100], train loss:0.0154
epoch [98/100], train loss:0.0117
epoch [99/100], train loss:0.0105
epoch [100/100], train loss:0.0097

Эпоха 50

Эпоха 100
Видим, что ошибки на аномальных и нормальных классах отличаются достаточно сильно. Сравним, как выглядят реальные и восстановленные данные:
# функция, которая возвращает восстановленные объекты
def get_prediction(model, x):
global batch_size
dataset = TensorDataset(torch.tensor(x.astype(np.float32)))
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=False)
predictions = []
for batch in data_loader:
x_batch = batch[0].cuda()
pred = model(x_batch) # x -> encoder -> decoder -> x_pred
predictions.append(pred.detach().cpu().numpy())
predictions = np.concatenate(predictions)
return predictions
# визуализация объектов из нескольких выборок (реальной и восстановленной)
def compare_data(xs, sample_num, data_range=(0, 1), labels=None):
fig, axes = plt.subplots(len(xs))
sample_size = len(xs[0][sample_num])
for i in range(len(xs)):
axes.plot(np.linspace(*data_range, sample_size), xs[sample_num])
if labels:
for i, label in enumerate(labels):
axes.set_ylabel(label)
Как модель отработает на нормальном примере:
x_test_pred = get_prediction(model, x_test)
compare_data([x_test[y_test == 0], x_test_pred[y_test == 0]], 10, labels=["real", "encoded"])
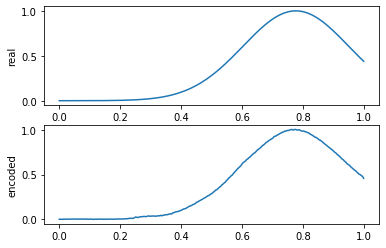
И на аномальном:

Что же делать с восстановленными X? Попробуем некоторые идеи.
Difference score
Самое очевидное — вычесть из аномального примера реальный. Тогда в том месте, где был второй пик, будет значение, большее нуля. И модель сможет легко это детектировать.
def get_difference_score(model, x):
global batch_size
dataset = TensorDataset(torch.tensor(x.astype(np.float32)))
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=False)
predictions = []
for (x_batch, ) in data_loader:
x_batch = x_batch.cuda()
preds = model(x_batch)
predictions.append(preds.detach().cpu().numpy())
predictions = np.concatenate(predictions)
# вычитание предсказанных примеров из реальных
return (x - predictions)
from sklearn.ensemble import RandomForestClassifier
test_score = get_difference_score(model, x_test)
score_forest = RandomForestClassifier(max_features=100)
score_forest.fit(test_score, y_test)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features=100,
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
Кстати, у читателя мог возникнуть вопрос: почему бы не сделать лишь 2 выборки — обучающую и тестовую. Так вот, в нашем пайплайне теперь 2 модели: сначала данные пропускаются через автоенкодер, затем — через функцию difference_score, и после — через случайный лес. Но если мы пропустим тренировочную выборку через автоенкодер, а затем подадим на обучение в случайный лес, то данные загрязнятся и работа модели будет некорректной.
Как это происходит? При обучении автоенкодер стремится минимизировать ошибку на обучающей выборке. Поэтому difference_score на ней будет очень низок, и случайный лес (вторая модель) будет думать, что нужно поставить низкий порог значений, чтобы сдетектировать аномалию. Но когда мы начнем тестировать валидационную выборку, может выясниться, что средний уровень difference_score на неаномальных объектах выше, чем при обучении (потому что автоенкодер не видел такие объекты при обучении). И случайный лес не сможет адекватно обнаружить аномалии.
Оценим модель на валидационной выборке:
val_score = get_difference_score(model, x_val)
prediction = score_forest.predict(val_score)
print(classification_report(y_val, prediction))
>>> precision recall f1-score support
0.0 0.76 1.00 0.87 100
1.0 1.00 0.69 0.82 100
accuracy 0.84 200
macro avg 0.88 0.84 0.84 200
weighted avg 0.88 0.84 0.84 200
Уже лучше. Посмотрим на наши данные:
indices = np.arange(len(prediction))
# в первую очередь нас интересуют те случаи, когда аномалии не были распознаны
wrong_indices = indices[(prediction == 0) & (y_val == 1)]
x_val_pred = get_prediction(model, x_val)
compare_data([x_val, x_val_pred], wrong_indices[0])
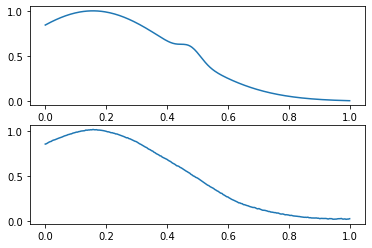
А что происходит с самими скорами? Нераспознанные аномалии:
plt.imshow(val_score[wrong_indices], norm=Normalize(0, 1, clip=True))

Распознанные аномалии:
plt.imshow(val_score[(prediction == 1) & (y_val == 1)], norm=Normalize(0, 1, clip=True))

И просто верно предсказанные неаномальные объекты:
plt.imshow(val_score[(prediction == 0) & (y_val == 0)], norm=Normalize(0, 1, clip=True))

Хм, это наталкивает на определенную мысль: у большей части аномальных объектов в скоре хорошо прослеживается пик.
Difference histograms
Тогда можно построить гистограммы значений и на них делать предсказания. У нормальных объектов столбцы будут находиться около нуля и встречаться относительно часто. У аномальных же — помимо основных столбцов, будут небольшие "побочные", соответствующие большей разнице между реальным и предсказанным объектом.
Посмотрим, в каком диапазоне изменяется difference score
print("test score: [{}; {}]".format(test_score.min(), test_score.max()))
>>> test score: [-0.2260764424351479; 0.26339245919832344]
Исходя из значений в тестовой выборке, будем строить гистограммы только на данном промежутке:
def score_to_histograms(scores, bins=10, data_range=(-0.3, 0.3)):
result_histograms = np.zeros((len(scores), bins))
for i in range(len(scores)):
hist, bins = np.histogram(scores, bins=bins, range=data_range)
result_histograms = hist
return result_histograms
test_histogram = score_to_histograms(test_score, bins=10, data_range=(-0.3, 0.3))
val_histogram = score_to_histograms(val_score, bins=10, data_range=(-0.3, 0.3))
plt.title("normal histogram")
plt.bar(np.linspace(-0.3, 0.3, 10), test_histogram[y_test == 0][0])

plt.title("anomaly histogram")
plt.bar(np.linspace(-0.3, 0.3, 10), test_histogram[y_test == 1][0])
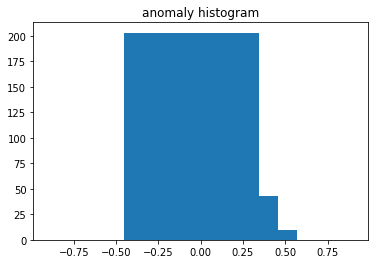
Действительно, появляется дополнительное "крыло", которое будет просто обнаружить.
histogram_forest = RandomForestClassifier(n_estimators=10)
histogram_forest.fit(test_histogram, y_test)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features='auto',
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
val_prediction = histogram_forest.predict(val_histogram)
print(classification_report(y_val, val_prediction))
>>> precision recall f1-score support
0.0 0.83 0.99 0.90 100
1.0 0.99 0.80 0.88 100
accuracy 0.90 200
macro avg 0.91 0.90 0.89 200
weighted avg 0.91 0.90 0.89 200
Выводы
Детектирование аномалий — сложная и интересная задача. Порой способы, которые работают на одном наборе данным, не будут работать на другом, пусть и очень похожем, датасете. Поэтому нужно смотреть на целые группы способов (подходы) и тестировать много гипотез.
Автокодировщики — очень мощный инструмент для детектирования аномалий. Что еще можно попробовать с ними? Есть вариант использовать VAE, у которого латентное пространство (те самые 4 нейрона) является нормальным распределением. Тогда можно классифицировать примеры по этому пространству. Также существуют CVAE, которые используют какой-то дополнительный признак для генерации из скрытого признакового пространства. Например, это может быть метка класса, размер цифры, максимальное значение в распределении и т.д.
Очень близко к автоенкодерам находятся GAN'ы, где есть целая модель (дискриминатор), позволяющая обнаружить семплы не из обучающей выборки. Тогда достаточно хорошо натренировать пару генератора и дискриминатора (что в действительности непросто).
Когда у меня впервые появилась задача детектировать аномалии, я составил небольшой список того, что можно попробовать.
Подходы для работы с картинками
Statistical parametric
Robust statistic
Non-parametric statistics
Neural networks
Немного обо мне
Меня зовут Евгений, Data science'ом я занимаюсь уже полтора года. Сейчас в большей степени погружаюсь в Computer vision, но также интересуюсь нейротехнологиями. (Соединить искусственные и натуральные нейронные сети — моя мечта!) Этот пост создан благодаря нашей команде — FARADAY Lab. Мы — начинающие российские стартаперы и готовы делиться с Вами тем, что узнаем сами.
Удачи c:

Полезные ссылки
Какой датасет выбрать?
Самый актуальный вопрос в жизни любого дата-саентиста. Чтобы упростить повествование, я буду использовать простой по структуре датасет, который сгенерируем здесь же.
# импортируем библиотеки
import os
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
# функция для генерации нормального распределения с заданными параметрами
def gen_normal_distribution(mu, sigma, size, range=(0, 1), max_val=1):
bins = np.linspace(*range, size)
result = 1 / (sigma * np.sqrt(2*np.pi)) * np.exp(-(bins - mu)**2 / (2*sigma**2))
cur_max_val = result.max()
k = max_val / cur_max_val
result *= k
return result
Рассмотрим пример работы функции. Создадим нормальное распределение с μ = 0.3 и σ = 0.05:
dist = gen_normal_distribution(0.3, 0.05, 256, max_val=1)
print(dist.max())
>>> 1.0
plt.plot(np.linspace(0, 1, 256), dist)

Объявим параметры нашего датасета:
in_distribution_size = 2000
out_distribution_size = 200
val_size = 100
sample_size = 256
random_generator = np.random.RandomState(seed=42) # для воспроизводимости используется seed
И функции для генерирования примеров — нормальных и аномальных. Нормальными будут считаться распределения с одним максимумом, аномальными — с двумя:
def generate_in_samples(size, sample_size):
global random_generator
in_samples = np.zeros((size, sample_size))
in_mus = random_generator.uniform(0.1, 0.9, size)
in_sigmas = random_generator.uniform(0.05, 0.5, size)
for i in range(size):
in_samples = gen_normal_distribution(in_mus, in_sigmas, sample_size, max_val=1)
return in_samples
def generate_out_samples(size, sample_size):
global random_generator
# создаем распределение с одним пиком
out_samples = generate_in_samples(size, sample_size)
# и накладываем поверх него еще один небольшой максимум
out_additional_mus = random_generator.uniform(0.1, 0.9, size)
out_additional_sigmas = random_generator.uniform(0.01, 0.05, size)
for i in range(size):
anomaly = gen_normal_distribution(out_additional_mus, out_additional_sigmas, sample_size, max_val=0.12)
out_samples += anomaly
return out_samples
Так выглядит нормальный пример:
in_samples = generate_in_samples(in_distribution_size, sample_size)
plt.plot(np.linspace(0, 1, sample_size), in_samples[42])

А аномальный — так:
out_samples = generate_out_samples(out_distribution_size, sample_size)
plt.plot(np.linspace(0, 1, sample_size), out_samples[42])

Создадим массивы с признаками и метками:
x = np.concatenate((in_samples, out_samples))
# нормальные примеры имеют метку 0, аномальные -- 1
y = np.concatenate((np.zeros(in_distribution_size), np.ones(out_distribution_size)))
# разделение на обучающую/тренировочную выборки
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, shuffle=True, random_state=42)
И позволю себе немного схитрить. Для алгоритмов, работающих в две стадии, потребуется 2 обучающих выборки и 1 тестовая (валидационная). При работе с реальными данными пришлось бы урезать имеющиеся тренировочную и тестовую выборки, но мы можешь догенерировать данные (в больших количествах), чтобы более объективно оценить качество модели:
# создаем валидационную выборку из 100 нормальных и 100 аномальных примеров
x_val_out = generate_out_samples(val_size, sample_size)
x_val_in = generate_in_samples(val_size, sample_size)
x_val = np.concatenate((x_val_out, x_val_in))
y_val = np.concatenate((np.ones(val_size), np.zeros(val_size)))
Модели
Перед тем, как перейти к теме статьи, проверим несколько алгоритмов детектирования аномалий из Sklearn: одноклассовый SVM и изолирующий лес. Это алгоритмы обучения без учителя, то есть они ориентируются только на представление данных, но не на обучающие метки.
# функции для оценки качества моделей
from sklearn.metrics import classification_report
from sklearn.metrics import f1_score
One class SVM
from sklearn.svm import OneClassSVM
OneClassSVM позволяет задать параметр nu — долю аномальных объектов в выборке.
out_dist_part = out_distribution_size / (out_distribution_size + in_distribution_size)
svm = OneClassSVM(nu=out_dist_part)
svm.fit(x_train, y_train)
>>> OneClassSVM(cache_size=200, coef0=0.0, degree=3, gamma='scale', kernel='rbf',
max_iter=-1, nu=0.09090909090909091, shrinking=True, tol=0.001,
verbose=False)
Делаем предсказания на тестовом наборе:
svm_prediction = svm.predict(x_val)
svm_prediction[svm_prediction == 1] = 0
svm_prediction[svm_prediction == -1] = 1
В sklearn есть очень удобная функция — classification_report, она позволяет оценить такие важные для Anomaly detection метрики, как precision и recall, причем для каждого класса:
print(classification_report(y_val, svm_prediction))
>>> precision recall f1-score support
0.0 0.57 0.93 0.70 100
1.0 0.81 0.29 0.43 100
accuracy 0.61 200
macro avg 0.69 0.61 0.57 200
weighted avg 0.69 0.61 0.57 200
Ну, такое. Довольно низкий f1-score свидетельствует о том, что модель плохо справляется с задачей.
Isolation forest
Окей, может быть, брат-близнец случайного леса сможет лучше справиться с задачей?
from sklearn.ensemble import IsolationForest
У изолирующего леса тоже есть параметр, отвечающий за долю аномальных объектов в выборке. Зададим его:
out_dist_part = out_distribution_size / (out_distribution_size + in_distribution_size)
iso_forest = IsolationForest(n_estimators=100, contamination=out_dist_part, max_features=100, n_jobs=-1)
iso_forest.fit(x_train)
>>> IsolationForest(behaviour='deprecated', bootstrap=False,
contamination=0.09090909090909091, max_features=100,
max_samples='auto', n_estimators=100, n_jobs=-1,
random_state=None, verbose=0, warm_start=False)
Classification report? — Classification report!
iso_forest_prediction = iso_forest.predict(x_val)
iso_forest_prediction[iso_forest_prediction == 1] = 0
iso_forest_prediction[iso_forest_prediction == -1] = 1
print(classification_report(y_val, iso_forest_prediction))
>>> precision recall f1-score support
0.0 0.50 0.91 0.65 100
1.0 0.53 0.10 0.17 100
accuracy 0.51 200
macro avg 0.51 0.51 0.41 200
weighted avg 0.51 0.51 0.41 200
RandomForestClassifier
Конечно, всегда стоит проверять какой-нибудь простой вариант типа "а вдруг задача классификации окажется посильной для случайного леса?" Что ж, попробуем:
from sklearn.ensemble import RandomForestClassifier
random_forest = RandomForestClassifier(n_estimators=100, max_features=100, n_jobs=-1)
random_forest.fit(x_train, y_train)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features=100,
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=-1, oob_score=False, random_state=None, verbose=0,
warm_start=False)
random_forest_prediction = random_forest.predict(x_val)
print(classification_report(y_val, random_forest_prediction))
>>> precision recall f1-score support
0.0 0.57 0.99 0.72 100
1.0 0.96 0.25 0.40 100
accuracy 0.62 200
macro avg 0.77 0.62 0.56 200
weighted avg 0.77 0.62 0.56 200
Autoencoder
В общем, случилась довольно обыденная для детектирования аномалий штука: ничего не сработало. Переходим к автокодировщикам.
Принцип работы автоенкодера состоит в том, что модель пытается сначала "сжать" данные, а потом восстановить их. Она состоит из 2 частей: Encoder'а и Decoder'а, которые занимаются сжатием и расшифровкой соответственно.

Изображение взято из
You must be registered for see links
Чтобы создать эффект "сжатия" данных, надо уменьшить скрытые слои, заставив их обрабатывать большее количество информации меньшим количеством нейронов.
Как этот эффект поможет нам? Теория информации говорит о том, что чем более вероятно событие, тем меньшее количество информации потребуется, чтобы описать это событие. Вспомним, что у нас всего лишь 9% аномалий и 91% нормальных объектов. Тогда для хранения информации об обычных объектах потребуется меньше информации, чем для запоминания аномальных. Но тогда, если мы подберем правильные параметры нейронной сети, то она сможет запоминать и восстанавливать только обычные объекты: на аномальные ей просто не будет хватать обобщающей способности.
Поэтому восстановленные моделью данные будут значительно отличаться от исходных.
Модель напишем на PyTorch, поэтому импортируем нужные модули:
import torch
from torch import nn
from torch.utils.data import TensorDataset, DataLoader
from torch.optim import Adam
Задаем гиперпараметры модели:
batch_size = 32
lr = 1e-3
Очень важная часть. Тренировочный датасет должен состоять только из обычных объектов, потому что если модель увидит аномальные, то она может "подстроиться" под их восстановление и мы не сможем найти значительные отличия в исходных и восстановленных данных. Конечно, когда гиперпараметры модели (количество нейронов в скрытых слоях, learning rate, размер батча) подобраны правильно, то шанс неудачи понижается, но лучше перестраховаться.
# берем только те примеры из x_train, которые не являются аномальными
train_in_distribution = x_train[y_train == 0]
train_in_distribution = torch.tensor(train_in_distribution.astype(np.float32))
train_in_dataset = TensorDataset(train_in_distribution)
train_in_loader = DataLoader(train_in_dataset, batch_size=batch_size, shuffle=True)
# для теста и валидации возьмем все примеры, чтобы можно было сравнивать работу модели на обычных и аномальных данных
test_dataset = TensorDataset(
torch.tensor(x_test.astype(np.float32)),
torch.tensor(y_test.astype(np.long))
)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
val_dataset = TensorDataset(torch.tensor(x_val.astype(np.float32)))
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
Моделька. Скрытый слой будет иметь размер 4 нейрона, чтобы сымитировать неоптимальные параметры модели (для обычных примеров нам достаточно 2 нейронов: один для задания μ, другой — для σ, так мы полностью опишем распределение; но вот 4 нейрона могут восстановить распределение с двумя максимумами, как в наших аномальных примерах).
class Autoencoder(nn.Module):
def __init__(self, input_size):
super(Autoencoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(input_size, 128),
nn.LeakyReLU(0.2),
nn.Linear(128, 64),
nn.LeakyReLU(0.2),
nn.Linear(64, 16),
nn.LeakyReLU(0.2),
nn.Linear(16, 4),
nn.LeakyReLU(0.2),
)
self.decoder = nn.Sequential(
nn.Linear(4, 16),
nn.LeakyReLU(0.2),
nn.Linear(16, 64),
nn.LeakyReLU(0.2),
nn.Linear(64, 128),
nn.LeakyReLU(0.2),
nn.Linear(128, 256),
nn.LeakyReLU(0.2),
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
model = Autoencoder(sample_size).cuda()
criterion = nn.MSELoss()
per_sample_criterion = nn.MSELoss(reduction="none") # loss для каждого примера, пропущенного через модель
# без параметра reduction="none" pytorch усредняет loss'ы по всем объектам
optimizer = Adam(model.parameters(), lr=lr, weight_decay=1e-5)
Чтобы как-то сравнивать loss'ы на нормальных и аномальных примерах, зададим функцию, строящую boxplot'ы ошибок:
def save_score_distribution(model, data_loader, criterion, save_to, figsize=(8, 6)):
losses = [] # здесь будем хранить loss для каждого объекта выборки
labels = [] # здесь -- метки класса
for (x_batch, y_batch) in data_loader:
x_batch = x_batch.cuda()
output = model(x_batch)
loss = criterion(output, x_batch)
loss = torch.mean(loss, dim=1) # усредняем loss по параметрам модели (то есть оставляем усредненную ошибку для каждого объекта выборки)
loss = loss.detach().cpu().numpy().flatten()
losses.append(loss)
labels.append(y_batch.detach().cpu().numpy().flatten())
losses = np.concatenate(losses)
labels = np.concatenate(labels)
losses_0 = losses[labels == 0] # нормальный класс
losses_1 = losses[labels == 1] # аномальный класс
fig, ax = plt.subplots(1, figsize=figsize)
ax.boxplot([losses_0, losses_1])
ax.set_xticklabels(['normal', 'anomaly'])
plt.savefig(save_to)
plt.close(fig)
На необученной модели функция выдает следующий результат:

Обучение:
experiment_path = "ood_detection" # папка для сохранения картинок
!rm -rf $experiment_path
os.makedirs(experiment_path, exist_ok=True)
epochs = 100
for epoch in range(epochs):
running_loss = 0
for (x_batch, ) in train_in_loader:
x_batch = x_batch.cuda()
output = model(x_batch)
loss = criterion(output, x_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
print("epoch [{}/{}], train loss:{:.4f}".format(epoch+1, epochs, running_loss))
# сохранение распределений ошибок
plot_path = os.path.join(experiment_path, "{}.jpg".format(epoch+1))
save_score_distribution(model, test_loader, per_sample_criterion, plot_path)
>>>
epoch [1/100], train loss:8.5728
epoch [2/100], train loss:4.2405
epoch [3/100], train loss:4.0852
epoch [4/100], train loss:1.7578
epoch [5/100], train loss:0.8543
...
epoch [96/100], train loss:0.0147
epoch [97/100], train loss:0.0154
epoch [98/100], train loss:0.0117
epoch [99/100], train loss:0.0105
epoch [100/100], train loss:0.0097

Эпоха 50

Эпоха 100
Видим, что ошибки на аномальных и нормальных классах отличаются достаточно сильно. Сравним, как выглядят реальные и восстановленные данные:
# функция, которая возвращает восстановленные объекты
def get_prediction(model, x):
global batch_size
dataset = TensorDataset(torch.tensor(x.astype(np.float32)))
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=False)
predictions = []
for batch in data_loader:
x_batch = batch[0].cuda()
pred = model(x_batch) # x -> encoder -> decoder -> x_pred
predictions.append(pred.detach().cpu().numpy())
predictions = np.concatenate(predictions)
return predictions
# визуализация объектов из нескольких выборок (реальной и восстановленной)
def compare_data(xs, sample_num, data_range=(0, 1), labels=None):
fig, axes = plt.subplots(len(xs))
sample_size = len(xs[0][sample_num])
for i in range(len(xs)):
axes.plot(np.linspace(*data_range, sample_size), xs[sample_num])
if labels:
for i, label in enumerate(labels):
axes.set_ylabel(label)
Как модель отработает на нормальном примере:
x_test_pred = get_prediction(model, x_test)
compare_data([x_test[y_test == 0], x_test_pred[y_test == 0]], 10, labels=["real", "encoded"])

И на аномальном:

Что же делать с восстановленными X? Попробуем некоторые идеи.
Difference score
Самое очевидное — вычесть из аномального примера реальный. Тогда в том месте, где был второй пик, будет значение, большее нуля. И модель сможет легко это детектировать.
def get_difference_score(model, x):
global batch_size
dataset = TensorDataset(torch.tensor(x.astype(np.float32)))
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=False)
predictions = []
for (x_batch, ) in data_loader:
x_batch = x_batch.cuda()
preds = model(x_batch)
predictions.append(preds.detach().cpu().numpy())
predictions = np.concatenate(predictions)
# вычитание предсказанных примеров из реальных
return (x - predictions)
from sklearn.ensemble import RandomForestClassifier
test_score = get_difference_score(model, x_test)
score_forest = RandomForestClassifier(max_features=100)
score_forest.fit(test_score, y_test)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features=100,
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
Кстати, у читателя мог возникнуть вопрос: почему бы не сделать лишь 2 выборки — обучающую и тестовую. Так вот, в нашем пайплайне теперь 2 модели: сначала данные пропускаются через автоенкодер, затем — через функцию difference_score, и после — через случайный лес. Но если мы пропустим тренировочную выборку через автоенкодер, а затем подадим на обучение в случайный лес, то данные загрязнятся и работа модели будет некорректной.
Как это происходит? При обучении автоенкодер стремится минимизировать ошибку на обучающей выборке. Поэтому difference_score на ней будет очень низок, и случайный лес (вторая модель) будет думать, что нужно поставить низкий порог значений, чтобы сдетектировать аномалию. Но когда мы начнем тестировать валидационную выборку, может выясниться, что средний уровень difference_score на неаномальных объектах выше, чем при обучении (потому что автоенкодер не видел такие объекты при обучении). И случайный лес не сможет адекватно обнаружить аномалии.
Оценим модель на валидационной выборке:
val_score = get_difference_score(model, x_val)
prediction = score_forest.predict(val_score)
print(classification_report(y_val, prediction))
>>> precision recall f1-score support
0.0 0.76 1.00 0.87 100
1.0 1.00 0.69 0.82 100
accuracy 0.84 200
macro avg 0.88 0.84 0.84 200
weighted avg 0.88 0.84 0.84 200
Уже лучше. Посмотрим на наши данные:
indices = np.arange(len(prediction))
# в первую очередь нас интересуют те случаи, когда аномалии не были распознаны
wrong_indices = indices[(prediction == 0) & (y_val == 1)]
x_val_pred = get_prediction(model, x_val)
compare_data([x_val, x_val_pred], wrong_indices[0])

А что происходит с самими скорами? Нераспознанные аномалии:
plt.imshow(val_score[wrong_indices], norm=Normalize(0, 1, clip=True))

Распознанные аномалии:
plt.imshow(val_score[(prediction == 1) & (y_val == 1)], norm=Normalize(0, 1, clip=True))

И просто верно предсказанные неаномальные объекты:
plt.imshow(val_score[(prediction == 0) & (y_val == 0)], norm=Normalize(0, 1, clip=True))

Хм, это наталкивает на определенную мысль: у большей части аномальных объектов в скоре хорошо прослеживается пик.
Difference histograms
Тогда можно построить гистограммы значений и на них делать предсказания. У нормальных объектов столбцы будут находиться около нуля и встречаться относительно часто. У аномальных же — помимо основных столбцов, будут небольшие "побочные", соответствующие большей разнице между реальным и предсказанным объектом.
Посмотрим, в каком диапазоне изменяется difference score
print("test score: [{}; {}]".format(test_score.min(), test_score.max()))
>>> test score: [-0.2260764424351479; 0.26339245919832344]
Исходя из значений в тестовой выборке, будем строить гистограммы только на данном промежутке:
def score_to_histograms(scores, bins=10, data_range=(-0.3, 0.3)):
result_histograms = np.zeros((len(scores), bins))
for i in range(len(scores)):
hist, bins = np.histogram(scores, bins=bins, range=data_range)
result_histograms = hist
return result_histograms
test_histogram = score_to_histograms(test_score, bins=10, data_range=(-0.3, 0.3))
val_histogram = score_to_histograms(val_score, bins=10, data_range=(-0.3, 0.3))
plt.title("normal histogram")
plt.bar(np.linspace(-0.3, 0.3, 10), test_histogram[y_test == 0][0])

plt.title("anomaly histogram")
plt.bar(np.linspace(-0.3, 0.3, 10), test_histogram[y_test == 1][0])

Действительно, появляется дополнительное "крыло", которое будет просто обнаружить.
histogram_forest = RandomForestClassifier(n_estimators=10)
histogram_forest.fit(test_histogram, y_test)
>>> RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features='auto',
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
val_prediction = histogram_forest.predict(val_histogram)
print(classification_report(y_val, val_prediction))
>>> precision recall f1-score support
0.0 0.83 0.99 0.90 100
1.0 0.99 0.80 0.88 100
accuracy 0.90 200
macro avg 0.91 0.90 0.89 200
weighted avg 0.91 0.90 0.89 200
Выводы
Детектирование аномалий — сложная и интересная задача. Порой способы, которые работают на одном наборе данным, не будут работать на другом, пусть и очень похожем, датасете. Поэтому нужно смотреть на целые группы способов (подходы) и тестировать много гипотез.
Автокодировщики — очень мощный инструмент для детектирования аномалий. Что еще можно попробовать с ними? Есть вариант использовать VAE, у которого латентное пространство (те самые 4 нейрона) является нормальным распределением. Тогда можно классифицировать примеры по этому пространству. Также существуют CVAE, которые используют какой-то дополнительный признак для генерации из скрытого признакового пространства. Например, это может быть метка класса, размер цифры, максимальное значение в распределении и т.д.
Очень близко к автоенкодерам находятся GAN'ы, где есть целая модель (дискриминатор), позволяющая обнаружить семплы не из обучающей выборки. Тогда достаточно хорошо натренировать пару генератора и дискриминатора (что в действительности непросто).
Когда у меня впервые появилась задача детектировать аномалии, я составил небольшой список того, что можно попробовать.
Подходы для работы с картинками
Statistical parametric
- GMM — Gaussian mixture modelling + Akaike or Bayesian Information Criterion
- HMM — Hidden Markov models
- MRF — Markov random fields
- CRF — conditional random fields
Robust statistic
- minimum volume estimation
- PCA
- estimation maximisation (EM) + deterministic annealing
- K-means
Non-parametric statistics
- histogram analysis with density estimation on KNN
- local kernel models (Parzen windowing)
- vector of feature matching with similarity distance (between train and test)
- wavelets + MMRF
- histogram-based measures features
- texture features
- shape features
- features from VGG-16
- HOG
Neural networks
- self organisation maps (SOM) or Kohonen's
- Radial Basis Functions (RBF) (Minhas, 2005)
- LearningVector Quantisation (LVQ)
- ProbabilisticNeural Networks (PNN)
- Hopfieldnetworks
- SupportVector Machines (SVM)
- AdaptiveResonance Theory (ART)
- Relevance vector machine (RVM)
Немного обо мне
Меня зовут Евгений, Data science'ом я занимаюсь уже полтора года. Сейчас в большей степени погружаюсь в Computer vision, но также интересуюсь нейротехнологиями. (Соединить искусственные и натуральные нейронные сети — моя мечта!) Этот пост создан благодаря нашей команде — FARADAY Lab. Мы — начинающие российские стартаперы и готовы делиться с Вами тем, что узнаем сами.
Удачи c:

Полезные ссылки
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links


